TikZ：R7年度：第2回基礎学力テスト数学(平面図形)解説

こんにちは。今回の基礎学は要所要所で難しい問題があり，解きにくかったのかなと感じている次第です。それでは平面図形の問題やってみましょう。例のごとく相似，三平方の定理は未修ということで話を進めていきます。

平面図形

下の図のように，正方形ABCDの対角線ACの延長上に点Eをとり，線分DEをひく。線分DEを1辺とする正方形DEFGをつくり，点G，点C，点Eをそれぞれ結ぶ。次の(1)～(3)に答えなさい。

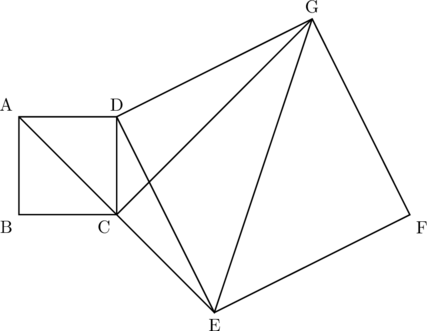
(1) $\sankaku{AED}\equiv\sankaku{CGD}$ であることを証明しなさい。
(2) $\kaku{CDE}=a\Deg$ のとき， $\kaku{CED}$ の大きさを $a$ を用いて表しなさい。
(3) $\sankaku{CEG}=36\text{cm}^2$ ， $\text{AC}=\text{CE}$ のとき，辺ABの長さを求めなさい。

解答・解説

(1) $\sankaku{AED}$ と $\sankaku{CGD}$ において，
仮定より，
$\text{AD}=\text{CD}\cdots\maru1$
$\text{DE}=\text{DG}\cdots\maru2$
$\kaku{ADE}=90\Deg+\kaku{CDE}\cdots\maru3$
$\kaku{CDG}=90\Deg+\kaku{CDE}\cdots\maru4$
$\maru3$ ， $\maru4$ より，
$\kaku{ADE}=\kaku{CDG}\cdots\maru5$
$\maru1$ ， $\maru2$ ， $\maru5$ より，2組の辺とその間の角がそれぞれ等しいので，
$\sankaku{AED}\equiv\sankaku{CGD}$

(2) $( 45-a )\Deg$

(3) $3\sqrt2\, \text{cm}$

【解説】
(2) 三角形の外角はその隣にない2つの内角の和に等しいので，
$\kaku{CDE}+\kaku{CED}=\kaku{ACD}\cdots\maru1$
ACは正方形の対角線より， $\kaku{ACD}=45\Deg$ ，また， $\kaku{CDE}=a\Deg$ より $\maru1$ は，
$a\Deg+\kaku{CED}=45\Deg$
よって，
$\kaku{CED}=( 45-a )\Deg$

(3) 三平方の定理は未修ということで解説します。

$\text{AC}=\text{CE}=x$ とおくと，(1)より $\text{AE}=\text{CG}=2x$ となる。
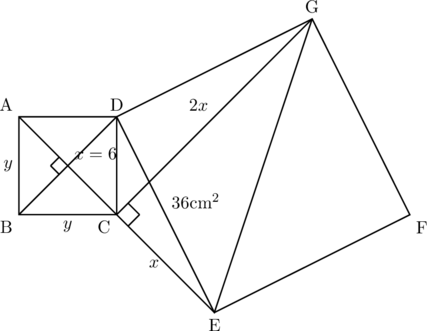
また，(1)より， $\kaku{DCG}=\kaku{DAE}=45\Deg$ であるから， $\kaku{GCE}=90\Deg$
$\sankaku{CEG}$ の面積の関係より，
$x\times2x\times\dfrac12=36$
$x^2=36$ ， $x>0$ より， $x=6$
ここで，点Bから対角線ACに垂線BHを引くと， $\text{BH}=3$ (ACの半分)であり，
$\text{AB}=\text{BC}=y$ とおくと， $\sankaku{ABC}$ の面積の関係から次の式が成り立つ。
$y\times y\times\dfrac12=6\times3\times\dfrac12$
$y^2=18$ ， $y>0$ より， $y=3\sqrt2$
よって，
$\text{AB}=3\sqrt2\, \text{cm}$

※三平方の定理で習う三角形の辺の比を知っていれば， $\text{AB}=6\div\sqrt2=3\sqrt2$ と平易に求まります。

平面図形

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル