おうぎ形の瞬殺技パート2です。大げさなことではないです。単に面積を求めるときの正方形の1辺を文字でおいただけです。それではどうぞ。
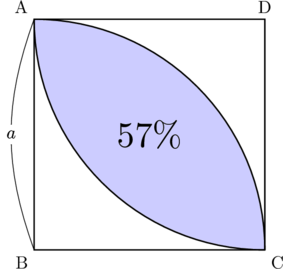
以下の図は,1辺の長さが![]() の正方形ABCDで,点B,点Dを中心として半径
の正方形ABCDで,点B,点Dを中心として半径![]() ,中心角
,中心角![]() のおうぎ形を正方形の内部にかいた図です。このとき,2つの弧によって囲まれる色のついた部分の面積を求めなさい。
のおうぎ形を正方形の内部にかいた図です。このとき,2つの弧によって囲まれる色のついた部分の面積を求めなさい。

上の設定では正方形の1辺の長さを文字![]() でおいてあるので,これを用いて面積を求めることで,一般化できます。
でおいてあるので,これを用いて面積を求めることで,一般化できます。
求め方は具体的な数字で問題を解くときと同じようにすればよいだけです。
解法は以下のようにするのが一般的でしょう。

おうぎ形ABCの面積を求めて,それから直角二等辺三角形ABCの面積を引いて求めた面積(色のついた部分)を2倍する。
したがって,次のようになる。
これを計算すると,色のついた部分の面積は,
色のついた部分の面積
色のついた部分の面積は![]() で求められる
で求められる
【例】1辺![]() の正方形なら,
の正方形なら,![]()
となる。
先に求めた,![]() であるが,算数の世界では
であるが,算数の世界では![]() なので,これで置き換えると,
なので,これで置き換えると,![]() となり,色のついた部分の面積は正方形の面積の約0.57倍であることが分かります。受験算数なんかでは有名らしいです。
となり,色のついた部分の面積は正方形の面積の約0.57倍であることが分かります。受験算数なんかでは有名らしいです。
 数樂管理人のブログ
数樂管理人のブログ 

