こんにちは。相城です。複素数の性質の中での拡大縮小回転の証明(補足)について書いておきます。高2で習う加法定理を用いますので以下の定理をご確認ください。
加法定理
2つの複素数の積
2つの複素数を以下のようにおきます。![]()
![]()
このとき, ![]() に
に![]() をかけることを考えると, 2つの複素数の積は,
をかけることを考えると, 2つの複素数の積は, 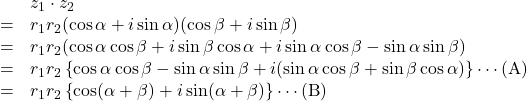
となり, 元の偏角![]() は
は![]() と
と![]() 増えていることが確認できます。また大きさ
増えていることが確認できます。また大きさ![]() は
は![]() 倍されていることが確認できます。すなわち, 2つの複素数の積は反時計回りに
倍されていることが確認できます。すなわち, 2つの複素数の積は反時計回りに![]() 回転させ, 大きさを
回転させ, 大きさを![]() 倍にする(拡大)ことを意味します。(A)⇒(B)に加法定理を用いています。
倍にする(拡大)ことを意味します。(A)⇒(B)に加法定理を用いています。
2つの複素数の商
今度は, ![]() を
を![]() で割ることを考えると, 2つの複素数の商は,
で割ることを考えると, 2つの複素数の商は, 
となり, 元の偏角![]() は
は![]() と
と![]() 減っていることが確認できます。また大きさ
減っていることが確認できます。また大きさ![]() は
は![]() 倍されていることが確認できます。すなわち, 2つの複素数の商は時計回りに
倍されていることが確認できます。すなわち, 2つの複素数の商は時計回りに![]() 回転させ, 大きさを
回転させ, 大きさを![]() 倍にすることを意味(縮小)します。(C)⇒(D)に加法定理を用いています。
倍にすることを意味(縮小)します。(C)⇒(D)に加法定理を用いています。
それでは。
 数樂管理人のブログ
数樂管理人のブログ 

