TikZ：中学数学：合同の証明と面積の割合

こんにちは。いい問題なので早速やってみましょう。

合同の問題と面積の割合

下の図のように，正三角形ABCの辺AB，BC，CA上にそれぞれ点D，E，Fを $\text{AD}=\text{BE}=\text{CF}$ となるようにとり，点Dと点E，Fをそれぞれ結ぶ。このとき，次の問いに答えなさい。

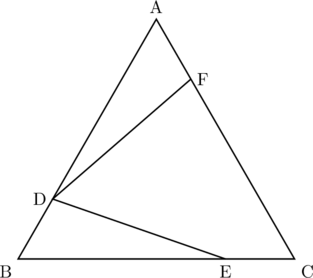
(1) $\sankaku{ADF}\equiv\sankaku{BED}$ であることを証明しなさい。
(2) 点Eと点Fを結ぶ。 $\text{AD} : \text{DB} = 3 : 1$ のとき， $\sankaku{ABC}$ の面積は， $\sankaku{DEF}$ の面積の何倍か求めなさい。

解答・解説

【解答】
(1) $\sankaku{ADF}$ と $\sankaku{BED}$ で，
仮定より，
$\text{AD}=\text{BE}\cdots\maru1$
$\text{AB}=\text{BC}=\text{CA}\cdots\maru2$
$\text{AD}=\text{BE}=\text{CF}\cdots\maru3$
$\maru2$ ， $\maru3$ より，
$\text{AF}=\text{BD}\cdots\maru4$
$\kaku{DAF}=\kaku{EBD}=60\Deg\cdots\maru5$
$\maru1$ ， $\maru4$ ， $\maru5$ より，
2組の辺とその間の角がそれぞれ等しいので，
$\sankaku{ADF}\equiv\sankaku{BED}$

(2) $\dfrac{16}{7}$ 倍

【解説】
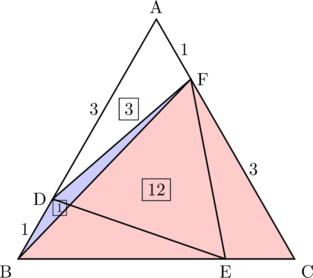
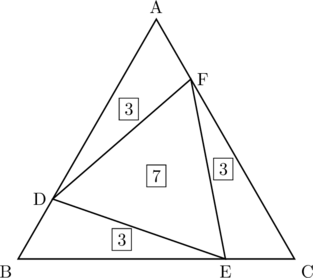
(2)
BとFを結んで考える。
$\text{AD} : \text{DB} = 3 : 1$ より， $\sankaku{ADF}$ と $\sankaku{BDF}$ の面積比は $\fbox{3} : \fbox{1}$ ，したがって， $\sankaku{ABF}=\fbox{4}$ ，同様に考えて， $\text{CF} : \text{FA}=3 : 1$ で， $\sankaku{ABF}=\fbox{4}$ であるから， $\sankaku{BCF}=\fbox{12}$ 。よって， $\sankaku{ABC}=\fbox{4}+\fbox{12}=\fbox{16}$ 。
ここで， $\sankaku{ADF}=\sankaku{BDE}=\sankaku{CFE}=\fbox{3}$ なので， $\sankaku{DEF}=\fbox{16}-\fbox{3}\times3=\fbox{7}$ 。
以上より， $\sankaku{ABC}=\fbox{16}$ ， $\sankaku{DEF}=\fbox{7}$ なので，求める答えは，
$\fbox{16}\div\fbox{7}=\dfrac{16}{7}$ (倍)

合同の問題と面積の割合

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル