TikZ：2019年度・埼玉県：空間図形

こんにちは。相城です。TikZの挙動がおかしく、右往左往しながら勉強しております。慣れるまではしばらくTikZで更新してまいります。いまのところemathってやはりすごいなぁって改めて驚いております。emathとTikZが融合して世界標準になればいいのになと思っています。正直今のところ私が使う分にはemathで十分間に合います。それでは2019年度埼玉県の空間図形の問題をどうぞ。

埼玉県

下の図1のような、正方形ABCDを底面とし、OA $=$ OB $=$ OC $=$ ODの正四角錐OABCDがあります。頂点Oから底面の正方形ABCDに垂線をひき、底面の正方形ABCDとの交点をHとします。
このとき、次の各問いに答えなさい。
(1)　△OHAと△OHBが合同であることを証明しなさい。
(2)　底面の正方形ABCDの1辺の長さが6cm、OA $=$ OB $=$ OC $=$ OD $=$ 6cmのとき、次の①、②に答えなさい。
①　線分OHの長さを求めなさい。
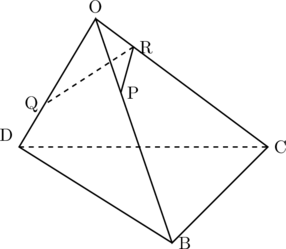
②　下の図2のように、正四角錐OABCDを3点O、B、Dを通る平面で切って、三角錐OBCDの辺OB上にOP $=$ 2cmとなる点P、辺OD上にOQ $=$ 4cmとなる点Qをとります。辺OC上に点Rをとり、PR $+$ RQの長さが最も短くなるとき、三角錐OPRQの体積を途中の説明も書いて求めなさい。

図1

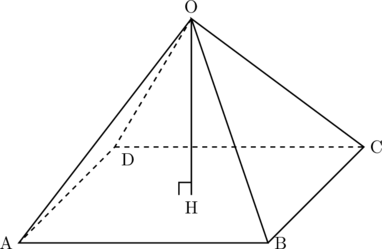
図2

答え

(1)　△OHAと△OHBで
仮定より, OA $=$ OB・・・①
共通な辺より
OH $=$ OH・・・②
正方形の対角線の長さは等しく, 対角線はそれぞれの中点で交わるので
AH $=$ BH・・・③
①, ②, ③より3組の辺がそれぞれ等しいので
△OHA≡△OHB
＊または∠OHA $=$ ∠OHB $=$ 90 $^{\circ}$
から直角三角形の斜辺と他の1辺がそれぞれ等しいでも可
(2)
①　△OHAで三平方の定理でOHを求める。
OA $=6$ cm、AH $=6\sqrt{2}\div2=3\sqrt{2}$
よってOH $=\sqrt{6^2-3\sqrt{2}^2}=3\sqrt{2}$
$3\sqrt{2}$ cm・・・答え
②

Rendered by QuickLaTeX.com

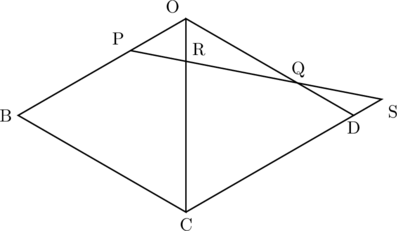
上図のように、線分PQが最短になるとき。
CDとPQを延長して交点をSとすると
△POQ∽△SDQで相似比が2 : 1(OQ : DQ)であるから
SD $=$ 1となるのでCS $=$ 7となる。
このとき△POR∽SCRとなり, 相似比はPO：SC $=$ 2 : 7なので
OR : CR $=$ 2 : 7となる。
よって三角錐OPRQは三角錐OBCDの
$\dfrac{1\times2\times2}{3\times9\times3}=\dfrac{4}{81}$ 倍
三角錐OBCDの体積は正四角錐OABCDの $\dfrac{1}{2}$ なので
三角錐OBCDの体積 $=6^2\times3\sqrt{2}\times\dfrac{1}{3}\times\dfrac{1}{2}=18\sqrt{2}$
求める体積はこれの $\dfrac{4}{81}$ 倍。よって
よって三角錐OPRQ $=18\sqrt{2}\times\dfrac{4}{81}=\dfrac{8\sqrt{2}}{9}$
$\dfrac{8\sqrt{2}}{9}$ cm $^3$ ・・・答え

埼玉県

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル