こんにちは。相城です。さて2020年度3月10日に行われた徳島県の高校入試の問題からです。それではどうぞ。
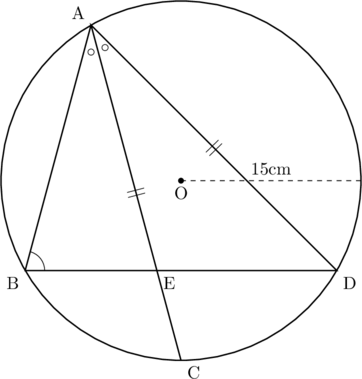
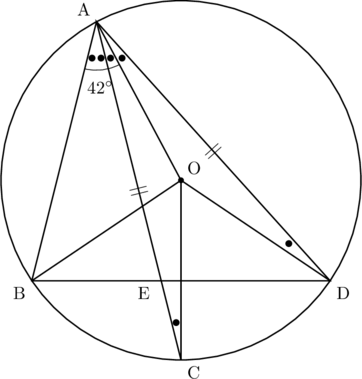
下の図のように、半径が15cmの円Oの周上に4点A,B,C,Dがあり,AC=ADである。また,弦ACは![]() の二等分線であり,弦ACと弦BDの交点をEとする。(1)~(3)に答えなさい。ただし,円周率は
の二等分線であり,弦ACと弦BDの交点をEとする。(1)~(3)に答えなさい。ただし,円周率は![]() とします。
とします。
(1) ![]() のとき,(a),(b)に答えなさい。
のとき,(a),(b)に答えなさい。
(a) ![]() の大きさを求めなさい。
の大きさを求めなさい。
(b) 点Aを含まないおうぎ形OBCの面積を求めなさい。
(2) ![]() を証明しなさい。
を証明しなさい。
(3) 点Cを含まない![]() の長さが
の長さが![]() cmのとき,点Bを含まない弧ADの長さを求めなさい。
cmのとき,点Bを含まない弧ADの長さを求めなさい。

答え
(1)
(a)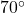
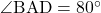 とする。CDを結ぶと△ACDが頂角
とする。CDを結ぶと△ACDが頂角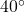 ,底角
,底角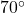 の二等辺三角形になり,
の二等辺三角形になり,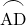 に対する円周角より,
に対する円周角より,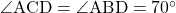
(b)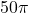 cm
cm

よって,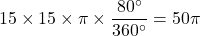
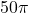 cm
cm
(2)
△ABCと△AEDで,
仮定より
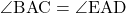 ・・・①
・・・①
AC AD・・・②
AD・・・②
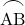 に対する円周角は等しいので,
に対する円周角は等しいので,
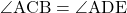 ・・・③
・・・③
①、②、③より,1組の辺とその両端の角がそれぞれ等しいので,
△ABC △AED
△AED
(3)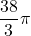 cm
cm
AとO、BとO、DとOを結ぶ。
中心角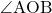 は
は
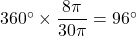
このとき,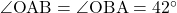
△OAC △OADとなり
△OADとなり とおくと,
とおくと,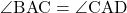 より,
より,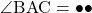 。このとき,
。このとき, であるから,
であるから,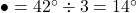 。よって,
。よって,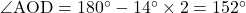
ゆえに,
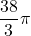 cm
cm
(a)
(b)
よって,
(2)
△ABCと△AEDで,
仮定より
AC
①、②、③より,1組の辺とその両端の角がそれぞれ等しいので,
△ABC
(3)
AとO、BとO、DとOを結ぶ。
中心角
このとき,
△OAC
ゆえに,
 数樂管理人
数樂管理人
この解き方以外でも解くことが可能です。以下のリンクからご覧ください。皆はどの解き方かな?
 TikZ:2020年度徳島県・こんなところに連立方程式の問題が
TikZ:2020年度徳島県・こんなところに連立方程式の問題が 数樂管理人のブログ
数樂管理人のブログ 

