こんにちは。相城です。今回は無理数ってホントどんな数字なの?ってことでお話ししていこうと思います。中学生の方は高校生の範囲を含んでいます。含んでいないところは読めるかもしれませんので, 楽しんでください。それではどうぞ。
無理数であることの証明
【問い】![]() が無理数であることを証明しなさい。
が無理数であることを証明しなさい。
このような問題が出てきたとき, 中学生の皆さんはどうされますか?
そもそも無理数って何なのでしょうね。答えを言うと循環しない無限小数です。これは何を意味するかというと, 分数で表わせない数だけど, 理屈をつけて考えたらあるんじゃないの? みたいな数です(概念として存在する)。ただ列記とした数であることは間違いなく, なくてはならないものです。
では, 先ほど存在しないと書きましたが, 存在するためにはどんな数でなければならないのでしょうか?
これが, この問題を解くカギになります。
皆さんが小学生, 中学生で習った数(![]() を除く)数は全部分数で表わせるのです。
を除く)数は全部分数で表わせるのです。
![]()
のように。
無理数などの実際存在しない数というのは, 分数で表わせないことを証明すればいいのです。
その手段として, 背理法(はいりほう)というのがあります。無理数が分数で表わせたと仮定して, 矛盾を見つける方法です。
以下に証明してみました。
ただし,
両辺を2乗して,
整理すると,
この式から,
よって,
このことは、
よって,
※お互いに1以外の約数を持たない⇒互いに素と言いますが, わかりやすくするために使っていません。ご了承ください。
これで証明終了です。
存在しないのに存在する
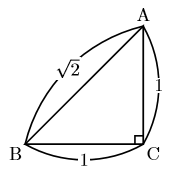
右の直角三角形を見てください。![]() の直角二等辺三角形です。
の直角二等辺三角形です。
言いたいことは存在しないはずの![]() が存在しているではありませんか。
が存在しているではありませんか。
では存在しない数なのに, なぜ![]() は図のように書くことができる(存在する)のでしょうか。
は図のように書くことができる(存在する)のでしょうか。
いろんな勉強をして僕なりの解釈を書きます。
まず![]() とはどういう数字か考えてみましょう。
とはどういう数字か考えてみましょう。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
このように![]() は有限小数としてあらわすことができます。
は有限小数としてあらわすことができます。
そして, これをずっと求めていくと真の![]() が求まるわけですが, それを小数で表わすことができないということです。
が求まるわけですが, それを小数で表わすことができないということです。
先の図のように![]() はどのくらいの長さか表わすことができます。ただ, それを小数で表わすことはできないということです。
はどのくらいの長さか表わすことができます。ただ, それを小数で表わすことはできないということです。
考えてみましょう。
![]() 以下小数第1億桁まで求めても有理数(有限小数)。 すなわち真の
以下小数第1億桁まで求めても有理数(有限小数)。 すなわち真の![]() 付近には無限の有理数が存在するのです。
付近には無限の有理数が存在するのです。
無理数はどう扱う?
では日常ではこの無理数をどう扱っているかというと, ![]() というアナログ(循環しない無限小数)をデジタル(循環しない有限小数, 近似値)として扱っているのです。 このように, 実際に存在しない数を扱う場合は, 近似値を使ってコンピュータなどで計算させます。
というアナログ(循環しない無限小数)をデジタル(循環しない有限小数, 近似値)として扱っているのです。 このように, 実際に存在しない数を扱う場合は, 近似値を使ってコンピュータなどで計算させます。
この近似値の精度を上げれば, より正確な値が得られます。ただ, コンピュータの処理時間はかかります。 音声処理や宇宙工学でも無理数は登場します。将来役に立たないかもしれませんが, それを使って仕事をして皆さんを支えてくれる人がいることを理解しましょうね。
 数樂管理人のブログ
数樂管理人のブログ 

