中学数学：中1規則性⑯

こんにちは。相城です。規則性の問題です。愛媛県の入試問題からです。それではどうぞ。

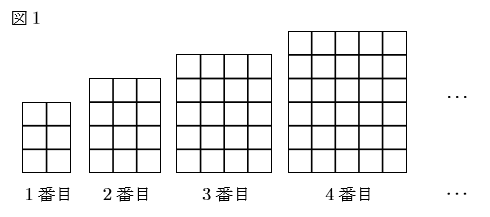
下の図1の, 1番目, 2番目, 3番目, 4番目,のように, 同じ大きさの正方形を規則的に並べて図形をつくり, それぞれの図形について, 並べた正方形の個数を調べ, 下のような表を作る。ただし, 図1の図形において, 太線はとなり合う正方形の共通な辺を表わしている。このとき, 次の問いに答えなさい。

(1) 表のア, イ, ウにあてはまる数をそれぞれ書きなさい。
(2) 12番目の図形において, 4辺が太線で表わされている正方形の個数は何個か。
(3) 番目の図形において, 3辺が太線で表わされている正方形の個数は何個か。を使って
表わしなさい。
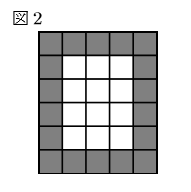
(4) 下の図2のように, 図形を作る正方形のうち, 外側に並ぶ正方形(をつけた正方形)について考えると, 4番目の図形では, その個数は18個である。外側に並ぶ正方形の個数が158個となるのは何番目の図形か。

【愛媛県】

解答pdf

プリントアウト用pdf