こんにちは。放物線と図形の基本問題?です。あんまりないパターンかもしれませんが, どうぞ。
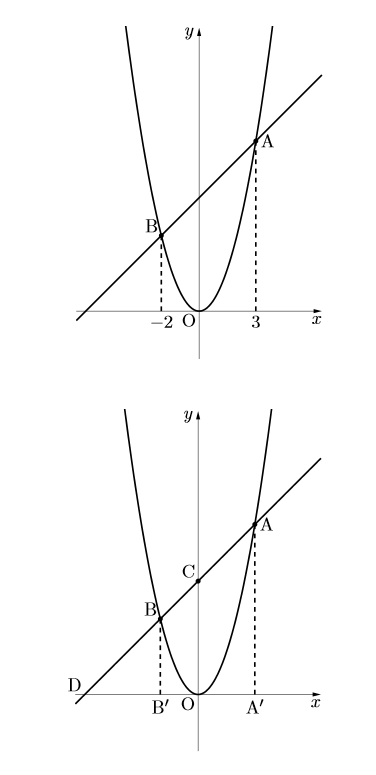
下の上図のように, 関数![]() 上のグラフ上に点A, Bがある。点A, Bの
上のグラフ上に点A, Bがある。点A, Bの![]() 座標がそれぞれ
座標がそれぞれ![]() ,
, ![]() であるとき, 次の問いに答えなさい。ただし, 原点をOとする。
であるとき, 次の問いに答えなさい。ただし, 原点をOとする。
(1) 点Aの![]() 座標を求めなさい。
座標を求めなさい。
(2) 直線ABの式を求めなさい。
(3) 関数![]() において,
において, ![]() の変域が
の変域が![]() のとき
のとき![]() の変域を
の変域を
求めなさい。
(4) 直線ABと![]() 軸,
軸, ![]() 軸との交点をそれぞれD, Cとし, 点A, Bから
軸との交点をそれぞれD, Cとし, 点A, Bから![]()
軸におろした垂線と![]() 軸との交点をそれぞれA
軸との交点をそれぞれA![]() , B
, B![]() とするとき,△DBB
とするとき,△DBB![]() と四角形BB
と四角形BB![]() OCと四角形COA
OCと四角形COA![]() Aの面積比を求めなさい。
Aの面積比を求めなさい。
 数樂管理人のブログ
数樂管理人のブログ 

