令和二年に徳島県で行われた第一回基礎学力テストからの出題。この問題は誘導が多いので, それに乗っかれば容易に解けたでしょう。
それでは問題です。一部表現など変えています。
次の表は「魔法陣」といって, どの縦, 横, 斜めの4つの数を加えても, 和が等しくなるようになっています。表のア~オに入る数を, ゆりさんとゆうとさんは考えています。

ゆりさんとゆうとさんは, 連立方程式を使って求めることができるのではないかと考えました。次の(1)~(3)に答えなさい。
(1) ゆりさんは次のように考えました。下の①, ②にあてはまる方程式を答えなさい。ただし, 式は簡単にしなくてよいものとします。
【ゆりさん】
私たちが学習したのは, 二元一次方程式だから, ア~オまでの中で2つを![]() ,
, ![]() として式をつくればよいね。
として式をつくればよいね。
イに入る数を![]() , オに入る数を
, オに入る数を![]() とすると,
とすると,
上から2行目の和と, 4行目の横の和が等しいから,
【 ① 】
また,
上から4行目の横の和と, 左から3列目の縦の和が等しいから,
【 ② 】
この①と②を連立方程式として解けばいいわ。
(2) ゆりさんのつくった連立方程式を解いて, イ, オにあてはまる数を答えなさい。
(3) ゆうとさんは, ゆりさんとはちがうところを![]() ,
, ![]() として考えました。次の①, ②にはア, ウ, エのどれかを, ③には連立方程式をかきなさい。ただし, 式は簡単にしなくてよいものとします。
として考えました。次の①, ②にはア, ウ, エのどれかを, ③には連立方程式をかきなさい。ただし, 式は簡単にしなくてよいものとします。
【ゆうとさん】
何を![]() と
と![]() とするかで, 連立方程式がつくれないときもあるから, 気をつけて考えよう。
とするかで, 連立方程式がつくれないときもあるから, 気をつけて考えよう。
僕は, 【①】を![]() , 【②】を
, 【②】を![]() とすると,
とすると,
【 ③ 】
のように, 連立方程式をつくることができたよ。
以上が問題です。

(1)は誘導通りに式をつくります。
①は以下の青の部分の和が等しいということなので
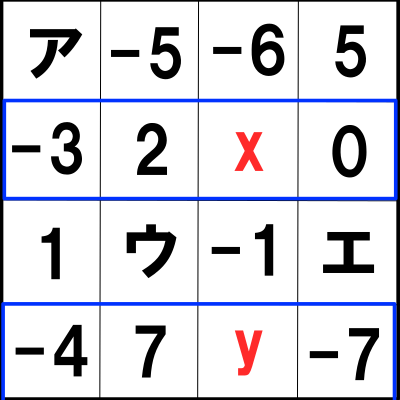
![]() ・・・(答)
・・・(答)
続いて②は以下の赤の部分が等しいということなので
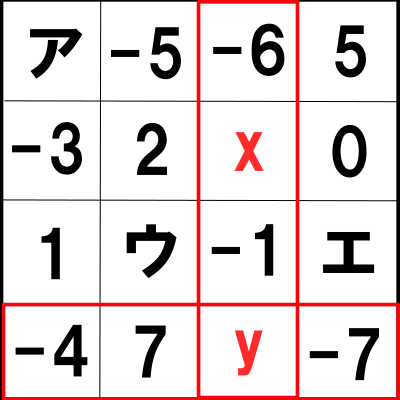
![]() ・・・(答)
・・・(答)
(2) (1)を整理して連立方程式をつくると
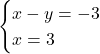
これを解いて, ![]()
イ.3, オ.6・・・(答)
一応確認ですが, 連立方程式の2つ目の式が一次方程式ですが, 何ら問題ありません。連立方程式はいくつかの方程式を組み合わせたものだからです。二元一次方程式でなければならないという決まりはありませんのでご注意を。
(3) 角アを文字で置くと, 一つは式ができますが, もう一つがつくれません。ただ(2)のゆりさんの解答を使えばア・ウ, ア・エでも答えとして成り立ちそうですが, ゆうとさんはゆりさんの答えを知らない。それは無しということなのでしょう。したがいまして, ①ウ(エ), ②エ(ウ)となります。
③の式に関しては下図をご参照ください。
縦の赤枠の和が等しいので![]()
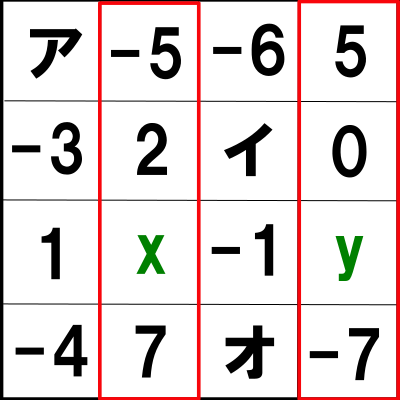
横の青枠と縦の青枠の和が等しいので![]()
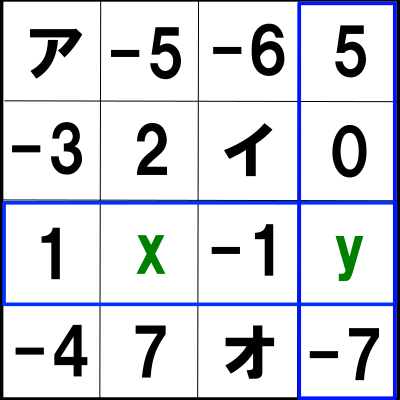
または次の縦の青枠と横の青枠の和が等しいので![]()
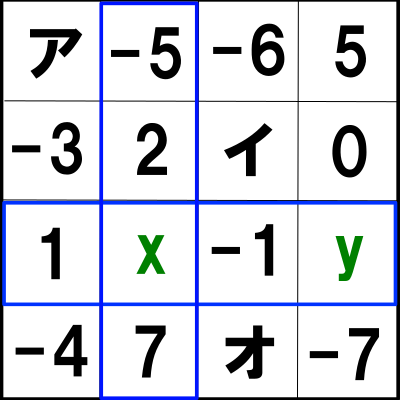
よって③は
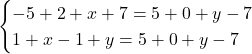
または
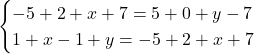
エが![]() で, ウが
で, ウが![]() のときは上の文字の
のときは上の文字の![]() を入れ替えてください。
を入れ替えてください。
 数樂管理人のブログ
数樂管理人のブログ 

