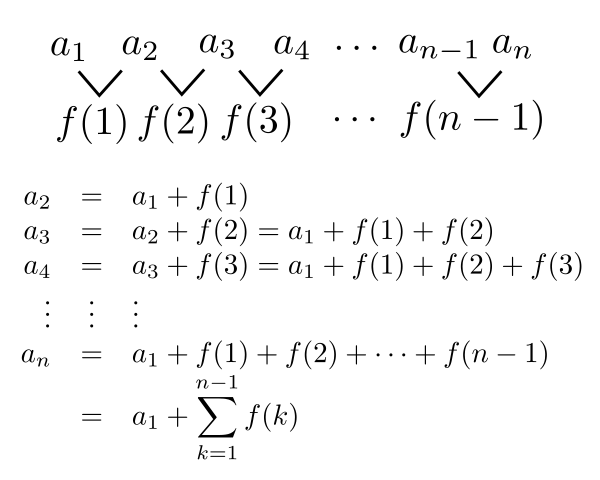こんにちは。相城です。今回は階差数列の漸化式について書いておきます。
今回の漸化式は等差数列の漸化式の発展版のようなものです。二項間の関係が数だけでなく式で表される場合のことになります。
一般的にこのことを![]() とし, 一般項
とし, 一般項![]() は,
は, ![]() として
として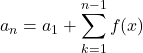
で得られます。これで求めた一般項が![]() のとき成り立つか考えて, 解答を得ます。※漸化式の
のとき成り立つか考えて, 解答を得ます。※漸化式の![]() の係数は1であることが前提になります。
の係数は1であることが前提になります。
仕組み的には以下のような感じです。
以下例題を見ながらやってみましょう。
例題を見てみよう
【例題】![]() ,
, ![]() で表される数列
で表される数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】![]() なので, 二項間の数が
なので, 二項間の数が![]() で表される数列になる。したがって, 一般項
で表される数列になる。したがって, 一般項![]() は,
は, ![]() として
として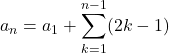
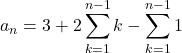
![]()
![]()
これは![]() のときも成り立つ。
のときも成り立つ。
よって, ![]() (答)
(答)
【例題】![]() ,
, ![]() で表される数列
で表される数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】前途した方法と同じく, 一般項![]() は,
は, ![]() として
として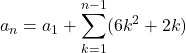
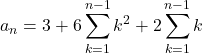
![]()
![]()
これは![]() のときも成り立つ。
のときも成り立つ。
よって, ![]() (答)
(答)
【例題】![]() ,
, ![]() で表される数列
で表される数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】もう慣れてきましたか?思考的には何ら変わりありません。
一般項![]() は,
は, ![]() として
として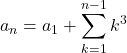
![]()
![]()
![]()
これは![]() のときも成り立つ。
のときも成り立つ。
よって, ![]() (答)
(答)
【例題】![]() ,
, ![]() で表される数列
で表される数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】これも二項間を表す数列が変わっただけで, 思考のロジックは同じです。
一般項![]() は,
は, ![]() として
として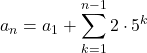
![]()
![]()
![]()
これは![]() のときも成り立つ。
のときも成り立つ。
よって, ![]() (答)
(答)
等差数列のときも同様に求められるよ
【例題】![]() ,
, ![]() で表される数列
で表される数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】等差数列の漸化式ですが, これも思考のロジックは同じで求められます。
一般項![]() は,
は, ![]() として
として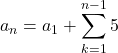
![]()
![]()
これは, ![]() のときも成り立つ。
のときも成り立つ。![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ