こんにちは。今回は3次関数の変曲点について触れておきます。
3次関数の2階微分
![]() の2次導関数
の2次導関数![]() って何を表すのでしょうか。基本的に
って何を表すのでしょうか。基本的に![]() となる点をそのグラフの変曲点といいます。ならない場合もあるので, 増減表を吟味してくださいね。
となる点をそのグラフの変曲点といいます。ならない場合もあるので, 増減表を吟味してくださいね。![]() が関数
が関数![]() の増減を表します。ということは
の増減を表します。ということは![]() は
は![]() の増減を表すということとして捉えておかしくはないでしょう。
の増減を表すということとして捉えておかしくはないでしょう。
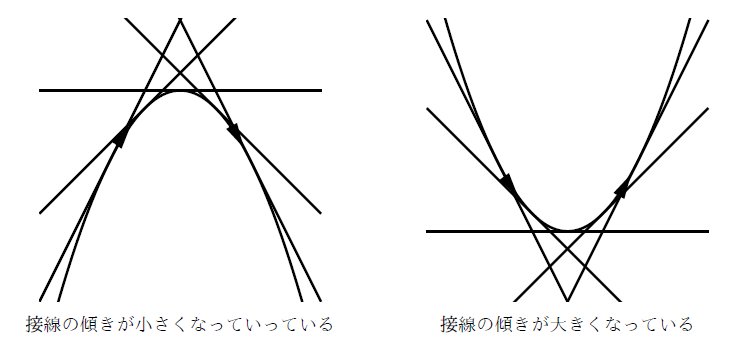
ここで![]() は接線の傾きを表す変数です。下の左の図のように接線の傾きが矢印の方向に小さくなっています。すなわち
は接線の傾きを表す変数です。下の左の図のように接線の傾きが矢印の方向に小さくなっています。すなわち![]() の値が減少しているときは, グラフは上に凸になっています。同様に右の図では接線の傾きが矢印の方向に大きくなっています。すなわち
の値が減少しているときは, グラフは上に凸になっています。同様に右の図では接線の傾きが矢印の方向に大きくなっています。すなわち![]() の値が増加しているときは, グラフは下に凸になっています。ちょうど車で言うとS字カーブをドリフトしているようなものでしょうか。変曲点はそのS字カーブでハンドルを切り替えるポイントのようなもの?じゃないでしょうか。
の値が増加しているときは, グラフは下に凸になっています。ちょうど車で言うとS字カーブをドリフトしているようなものでしょうか。変曲点はそのS字カーブでハンドルを切り替えるポイントのようなもの?じゃないでしょうか。
具体例を見ていこう
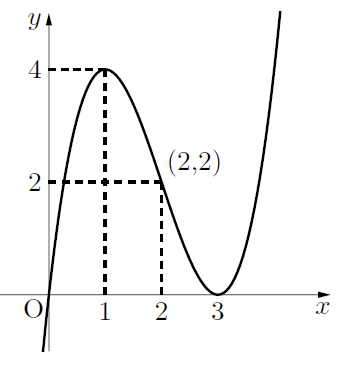
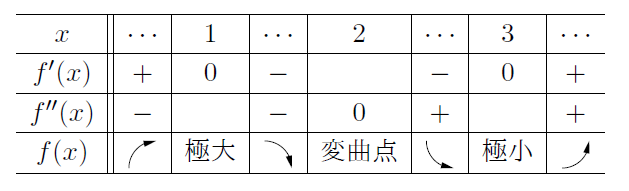
3次関数![]() のグラフの増減表と変曲点を書いてみました。
のグラフの増減表と変曲点を書いてみました。
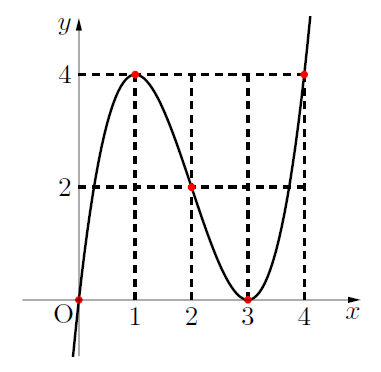
グラフは以下になります。(2,2)はこの関数の変曲点です。
以下に変曲点にまつわる話を書いておきます。
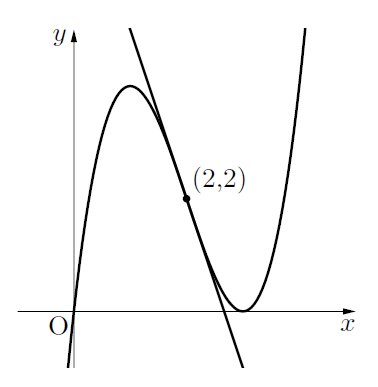
変曲点における接線
変曲点における接線はグラフを突き抜けます。後述しますが, 変曲点からは接線は1本しか引けません。
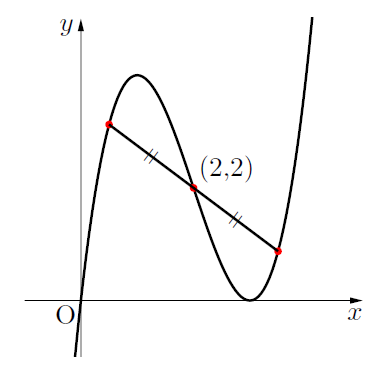
3次関数は変曲点について点対称
変曲点を通る直線とグラフの交点がある場合については, 変曲点について対称な位置関係にあります。
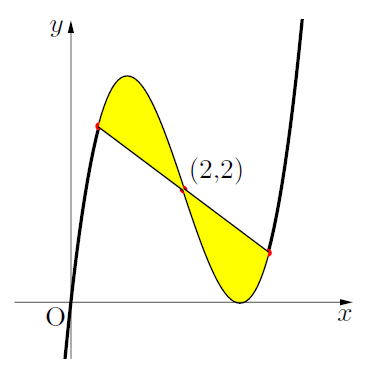
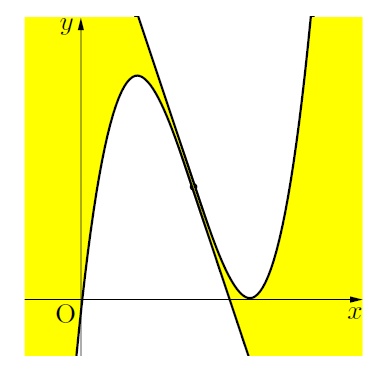
変曲点を通る線で囲まれた面積は等しい
変曲点を通る直線で, 囲まれた黄色の部分の面積は等しくなっています。
8つの合同な長方形で囲まれる
このように合同な長方形が8つできます。変曲点や極値などが角にあるのが分かるでしょう。
引ける接線の本数は決まってる
※描いてあるグラフは3次関数![]() と変曲点における接線
と変曲点における接線![]() になります。証明は下部の記事をご覧ください。
になります。証明は下部の記事をご覧ください。
②もとのグラフ上の1点, 変曲点における接線上の1点(変曲点は含まない)からは2本
③白の領域の1点, 変曲点からは1本の接線が引ける。
 数樂管理人のブログ
数樂管理人のブログ