こんにちは。相城です。
今回は角度の問題をピックアップ。
問題は次のようになります。解説はその下にありますので見たくない人は問題だけご覧ください。
下の図のような△ABCがあり、点Dは![]() の二等分線と辺BCとの交点である。
の二等分線と辺BCとの交点である。
DA![]() DB、
DB、![]() のとき、
のとき、![]() の大きさを求めなさい。
の大きさを求めなさい。
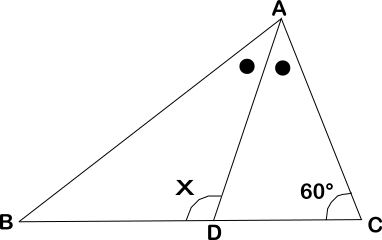
それでは解説です。
DA![]() DBより△ABDは二等辺三角形で、
DBより△ABDは二等辺三角形で、![]() で、三角形の外角の定理より、
で、三角形の外角の定理より、![]() となります。図で表すと以下のようになります。
となります。図で表すと以下のようになります。
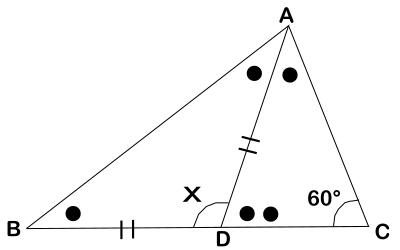
![]() だとわかりにくいかもしれないので、下の図のように
だとわかりにくいかもしれないので、下の図のように![]() を
を![]() で置き換えます。
で置き換えます。
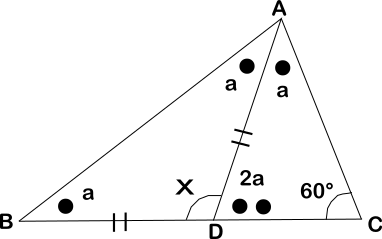
このとき△ADCで三角形の内角の関係により、![]()
![]()
![]()
よって![]() ADC
ADC![]() となり、
となり、![]() となります。もちろん、
となります。もちろん、![]() でも大丈夫です。
でも大丈夫です。
答え100![]()
 数樂管理人のブログ
数樂管理人のブログ 

