こんにちは。相城です。
さて、今回は放物線の問題をやってみようと思います。
今回の問題は4つの問題のうち3つは取っておきたい問題となっていますので、数学が苦手な方も取り組んでほしいと思います。
それでは問題です。
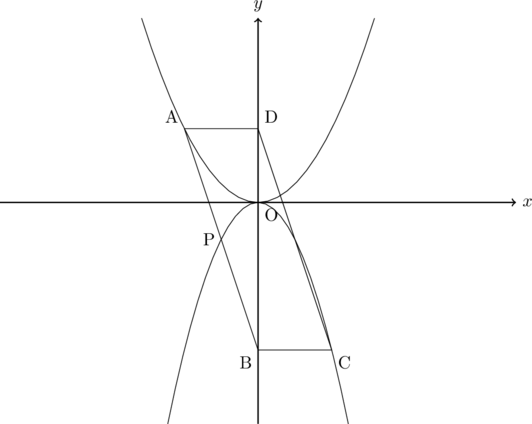
問い:下の図のように、点Aは関数![]() のグラフ上にあり、Aの
のグラフ上にあり、Aの![]() 座標は
座標は![]() である。また、点B、Dは
である。また、点B、Dは![]() 軸上、点Cは関数
軸上、点Cは関数![]() のグラフ上にある。点Pは関数
のグラフ上にある。点Pは関数![]() のグラフと線分ABの交点で、その座標は(
のグラフと線分ABの交点で、その座標は(![]() ,
, ![]() )である。
)である。
四角形ABCDが平行四辺形で、ADと![]() 軸が平行になるとき、次の(1)~(3)に答えなさい。
軸が平行になるとき、次の(1)~(3)に答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) 点Bの座標を求めなさい。
(3) △PCDの面積を求めなさい。
(4) 点Aを通る直線で平行四辺形ABCDの面積を2 : 1に分ける。その直線と平行四辺形ABCDとの交点をQとするとき、直線AQの傾きをすべて求めなさい。
以上が問題になります。

解説は以下に書いていきますのでご覧になってください。
(1) P(![]() ,
, ![]() )は関数
)は関数![]() 上の点なので、代入すると、
上の点なので、代入すると、![]() (答え)となる。
(答え)となる。
(2) 点Bは直線APの切片なので、直線APを求めることに専念する。
点A(![]() )、P(
)、P(![]() ,
,![]() )なので、直線APは
)なので、直線APは![]() となるので、点Bの座標は(
となるので、点Bの座標は(![]() )
)![]() (答え)
(答え)
(3) △PCDの面積を次のように考える。
△PCD![]() 平行四辺形ABCD-△APD-△PBC
平行四辺形ABCD-△APD-△PBC
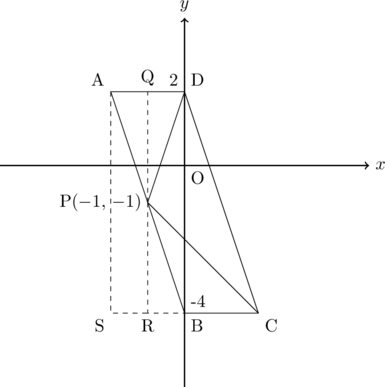
上図より平行四辺形ABCDは底辺がBC![]() 2、高さがAS
2、高さがAS![]() 6なので面積は
6なので面積は![]() 、△APDは底辺AD
、△APDは底辺AD![]() 2、高さPQ
2、高さPQ![]() 3なので、面積は
3なので、面積は![]() 、△PBCは底辺BC
、△PBCは底辺BC![]() 2、高さPR
2、高さPR![]() 3なので、面積は
3なので、面積は![]() 。よって△PCDの面積は、
。よって△PCDの面積は、
△PCD![]() 12-3-3
12-3-3![]() 6
6![]() (答え)
(答え)
(4) 【方針】(3)より平行四辺形ABCDの面積は12であるから、2 : 1に分けるということは全体を3等分することを考えればいいので、1に当たる面積は![]() になる。したがって下図の△ABMが4になる場合と、△ADNが4になる場合を考えればよい。
になる。したがって下図の△ABMが4になる場合と、△ADNが4になる場合を考えればよい。
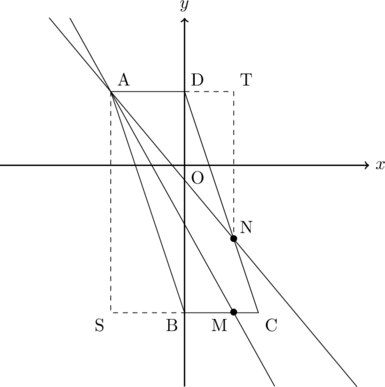
さて、△ABMが4になる場合底辺はBMになるのですが、長さが分かっていないので![]() として求めることにします。高さはAS
として求めることにします。高さはAS![]() 6なので、
6なので、![]() とすると、
とすると、![]() となり、M
となり、M![]() となるので、直線AMの傾きは
となるので、直線AMの傾きは![]()
次に、△ADNが4になる場合、底辺はAD![]() 2となるので、高さTNが分かっていないので、TN
2となるので、高さTNが分かっていないので、TN![]() とおいて求めると、
とおいて求めると、![]() として、
として、![]() となる。したがって、Nの
となる。したがって、Nの![]() 座標はTの
座標はTの![]() 座標2から4下に行ったところになるので、
座標2から4下に行ったところになるので、![]() になる。この
になる。この![]() という
という![]() 座標は直線DC上にあるので、直線DCを求めると、D
座標は直線DC上にあるので、直線DCを求めると、D![]() 、C
、C![]() より、
より、![]() であるから、
であるから、![]() を代入し、
を代入し、![]() 座標を求めると
座標を求めると![]() となる。よってN
となる。よってN![]() であるから、直線ANの傾きは
であるから、直線ANの傾きは![]()
以上より、求める傾きは![]() 、
、![]() (答え)
(答え)
座標が分数のとき、直線の傾きや式を求めるときは、直線の式を![]() として、2点の座標を代入して、連立方程式で求めるといいでしょう。
として、2点の座標を代入して、連立方程式で求めるといいでしょう。
それではお粗末でした。
 数樂管理人のブログ
数樂管理人のブログ 

