こんにちは。相城です。さて, 今回は富山県の高校入試から平面図形の問題をピックアップ。TikZの練習題材として選びました。今回これをつくるにあたってはコンパスを用いた三角形の書き方を用いました。なんとなくではありますが, 感覚はつかめたかと思います。ただ, 外接円は今回用いていません。初めにつまずきすぎて, それを考える余裕がなくなってしまいました。したがって, 今回のこの円は正三角形の重心を中心として点Aを通る円として書いております。それでは問題です。
図1のように, 円Oの周上に点A, B, C, Dがあり, △ABCは正三角形である。また線分BD上に, BE![]() CDとなる点Eをとる。このとき, 次の問いに答えなさい。
CDとなる点Eをとる。このとき, 次の問いに答えなさい。
(1) △ABE≡△ACDを証明しなさい。
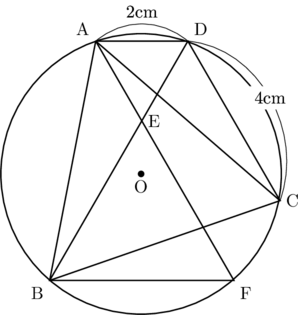
(2) 図2のように線分AEの延長と円Oとの交点をFとし, AD![]() 2cm, CD
2cm, CD![]() 4cmとするとき, 次の問いに答えなさい。
4cmとするとき, 次の問いに答えなさい。
① △BFEの面積を求めなさい。
② 線分BCの長さを求めなさい。
図1
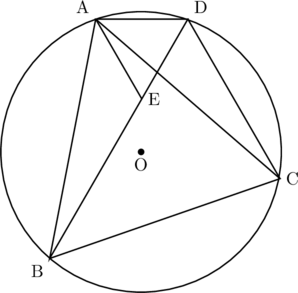
図2

答え
(1)
△ABEと△ACDで,
仮定より
BE=CD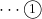
△ABCは正三角形だから
AB=AC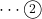
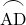 に対する円周角は等しいので
に対する円周角は等しいので
∠ABE=∠ACD
 より、2組の辺とその間の角がそれぞれ等しいので,
より、2組の辺とその間の角がそれぞれ等しいので,
△ABE≡△ACD
(2)
①1辺が4㎝の正三角形になる。
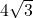 cm
cm
②点Cと点Fを結ぶと, ∠BFC=120 。
。
点CからBFの延長線上に垂線を下ろして, 30 , 90
, 90 , 60
, 60 の三角形を作って考える。そして三平方の定理よりBCを直接求める。
の三角形を作って考える。そして三平方の定理よりBCを直接求める。
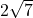 cm
cm
△ABEと△ACDで,
仮定より
BE=CD
△ABCは正三角形だから
AB=AC
∠ABE=∠ACD
△ABE≡△ACD
(2)
①1辺が4㎝の正三角形になる。
②点Cと点Fを結ぶと, ∠BFC=120
点CからBFの延長線上に垂線を下ろして, 30
 数樂管理人のブログ
数樂管理人のブログ 

