こんにちは。相城です。ユーグリッドの互除法を使って求めるパターンを置いておきます。それではどうぞ。
(1) ![]() を満たす整数
を満たす整数![]() の組を1つ見つけよ。
の組を1つ見つけよ。
(2) ![]() を満たすすべての整数解を求めよ。
を満たすすべての整数解を求めよ。
(3) ![]() を満たす整数
を満たす整数![]() の組を1つ見つけよ。
の組を1つ見つけよ。
(4) ![]() を満たす整数
を満たす整数![]() の組を1つ見つけよ。
の組を1つ見つけよ。

答え
(1)
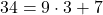 より
より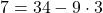 ・・・①
・・・①
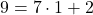 より
より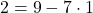 ・・・②
・・・②
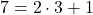 より
より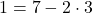 ・・・③
・・・③
②を③にあてはめて,
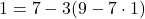
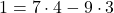
これに①をあてはめて,
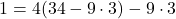
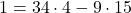
よって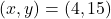
(2)
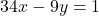 と
と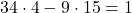 を筆算でひくと,
を筆算でひくと,
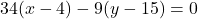 となり、34と9は互いに素だから,
となり、34と9は互いに素だから,
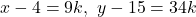 とおける。
とおける。
よって求める整数解は、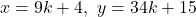 (
(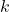 は整数)
は整数)
となる。
(3)
(1)より、(1)の答えを5倍したものが答え。よって, この場合,
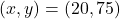 が答え。
が答え。
(4)
まず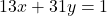 を満たす整数
を満たす整数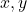 の組を1組見つけて3倍することを考える。
の組を1組見つけて3倍することを考える。
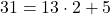 より
より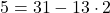 ・・・①
・・・①
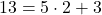 より
より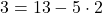 ・・・②
・・・②
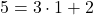 より
より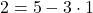 ・・・③
・・・③
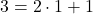 より
より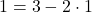 ・・・④
・・・④
④に③をあてはめて,
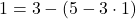
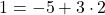
これに②をあてはめて,
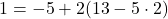
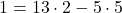
これに①をあてはめて,
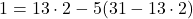
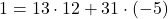
よって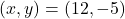 であるから,
であるから,
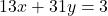 を満たす整数
を満たす整数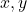 の1組は
の1組は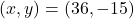
②を③にあてはめて,
これに①をあてはめて,
よって
(2)
よって求める整数解は、
となる。
(3)
(1)より、(1)の答えを5倍したものが答え。よって, この場合,
(4)
まず
④に③をあてはめて,
これに②をあてはめて,
これに①をあてはめて,
よって
 数樂管理人のブログ
数樂管理人のブログ 

