高1での内分点、外分点の求め方

こんにちは。相城です。高1生で習う内分点、外分点の話ですが、公式があります。しかし、それを習うのは高2のときです。じゃそれを習わないとした高1生はどう攻略していくかお話ししてい行きます。以下に例を示してお話ししていきます。

例題を見ていこう

【例】数直線上にA, Bがあります。
(1) ABを3 : 1に内分する点Pを求めよ。
(2) ABを2 : 3に外分する点Qを求めよ。
(3) ABを3 : 1に外分する点Rを求めよ。

内分点はさらっといっちゃいますね。ABが長さ4なので、それにをかけたをAから右に進めたところがPになります。よって、P　下図参照。

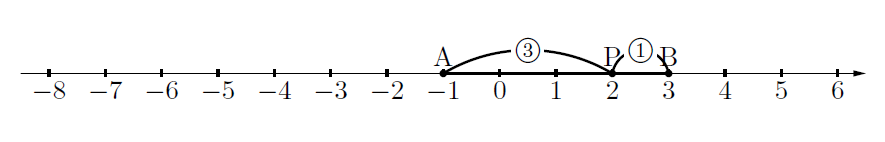
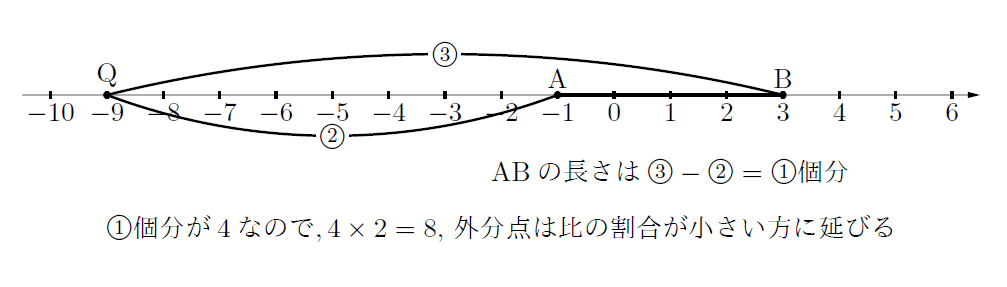
(2)の外分点の話ですが、ポイントは外分点は比の割合が小さい方にあるってことです。(2)では2 : 3に外分とあるので、比の割合が小さいのは、左側の2なので、数直線上では点Aより左側に点Qはあります。また、このときがABの長さ4と一致するので、左側に個分()延ばした点がQになります。したがって点Qの座標はQ　下図参照。

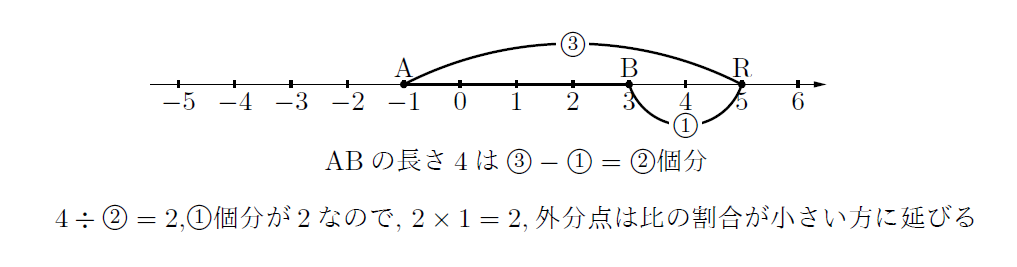
続いて(3)の外分点も同様です。3 : 1に外分とあるので、比の割合では1の方が小さいので、数直線上では点Bより右側に点Rはあります。また、このとき、がABの長さ4と一致するので、(個分)を右側に延ばした点がRになります。したがって、点Rの座標はR(5, 0)　下図参照。

今回は数直線を用いて内分点、外分点のお話をしましたが、平面上でも同じです。これに縦軸の軸、つまり縦の数直線が加わるだけですので、この基本を理解しておけばこれに関しては問題ないかと思います。余談ですが、高2で習う分点の公式はベクトルとかでも使うので、覚えた方がいいですよ。それでは。