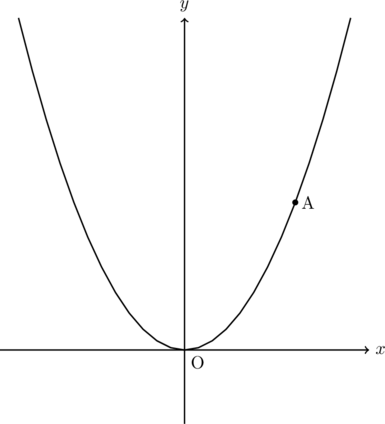
こんにちは。相城です。2020年2月の千葉県前期問題から放物線の問題です。それではどうぞ。
下の図もように、関数![]() のグラフ上に点Aがあり、点Aの座標は
のグラフ上に点Aがあり、点Aの座標は![]() である。ただし、
である。ただし、![]() とする。
とする。
このとき、次の(1)、(2)の問いに答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) ![]() 軸上に点Bを、OA
軸上に点Bを、OA![]() OBとなるようにとる。ただし、点Bの
OBとなるようにとる。ただし、点Bの![]() 座標は負とする。このとき、次の①、②の問いに答えなさい。
座標は負とする。このとき、次の①、②の問いに答えなさい。
① 2点A、Bを通る式を求めなさい。
② 原点Oを通り、直線ABに平行な直線を![]() とする。点Aから
とする。点Aから![]() 軸に垂線をひき、直線
軸に垂線をひき、直線![]() との交点をCとする。また、関数
との交点をCとする。また、関数![]() のグラフ上に、
のグラフ上に、![]() 座標が3より大きい点Dをとり、点Dから
座標が3より大きい点Dをとり、点Dから![]() 軸に垂線をひき、直線OAとの交点をE、直線
軸に垂線をひき、直線OAとの交点をE、直線![]() との交点をFとする。
との交点をFとする。
△AOCと四角形ACFEの面積の比が16 : 9となるとき、点Dの座標を求めなさい。

答え
(1) A(3, 4)より、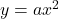 に代入して
に代入して
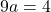
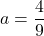
(2)
① OA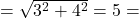 OB
OB
よって、B(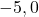 )となる。したがって直線ABは
)となる。したがって直線ABは
A(3, 4)、B(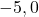 )を通る直線である。
)を通る直線である。
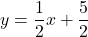
② 問題文を図式化すると以下のようになる。
(2)
① OA
よって、B(
A(3, 4)、B(
② 問題文を図式化すると以下のようになる。
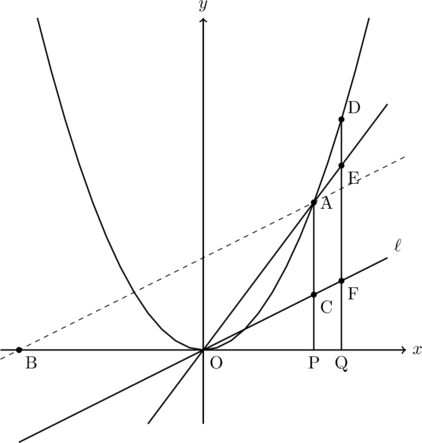
△AOC![]() ⑯、四角形ACFE
⑯、四角形ACFE![]() ⑨とすると、△EOFは⑯+⑨=㉕となる。このとき、△AOC∽△EOFとなり、面積比が⑯:㉕であるから、辺の比は4 : 5になる。
⑨とすると、△EOFは⑯+⑨=㉕となる。このとき、△AOC∽△EOFとなり、面積比が⑯:㉕であるから、辺の比は4 : 5になる。
このことから
OP : OQ![]() 4 : 5となり、OP
4 : 5となり、OP![]() 3であるから
3であるから
3 : OQ![]() 4 : 5
4 : 5
OQ![]()
![]() に
に![]() を代入して、
を代入して、![]()
したがって
D![]()
 数樂管理人のブログ
数樂管理人のブログ 

