TikZ：2020年度・埼玉県：相似な図形と三平方の定理の基本

こんにちは。相城です。タイトル通りですので、これ以上コメントしてネタバレになるといけないので、解いてみてください。それではどうぞ。

埼玉県の問題

次は、AさんとBさんの会話です。これを読んで、下の各問いに答えなさい。
Aさん「あの電柱の高さは、直角三角形の相似の考え方を使って求められそうだね。」
Bさん「影の長さを比較して求める方法だね。」
Aさん「電柱と比較するのに、校庭の鉄棒が利用できそうだね。」
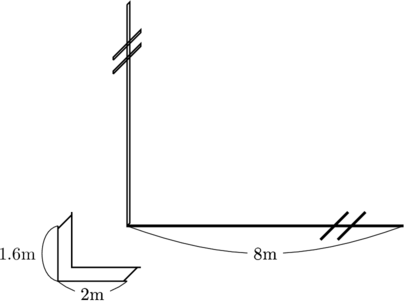
(1) AさんとBさんが、鉄棒の高さと影の長さ、電柱の影の長さを測ったところ、鉄棒の高さは1.6m、鉄棒の影の長さは2m、電柱の影の長さは8mでした。このとき、電柱の高さを求めなさい。
ただし、影の長さは同時刻に測ったものとし、電柱と鉄棒の幅や厚みは考えないものとします。また、電柱と鉄棒は地面に対して垂直に立ち、地面は平面であるものとします。

(2) AさんとBさんは、電柱よりも高い鉄塔の高さを求めようとしました。しかし、障害物があり、鉄塔の影の長さを測ることができないので先生に相談しました。先生は、影の長さを測らずに高さを求める方法を以下のように説明してくれました。
【ア】にあてはまる値を求めなさい。
『先生の説明』
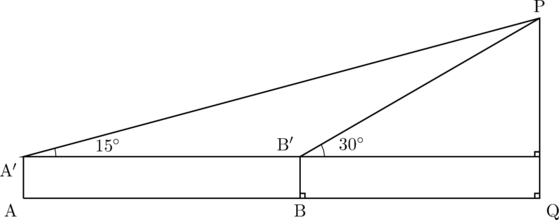
下の図のように、鉄塔の先端をPとし、Pから地面に垂線をひき、地面との交点をQとします。また、Aさんの立つ位置を点A、Aさんの目の位置を点A、Bさんの立つ位置をB、Bさんの目の位置をBとし、2人は水平な地面に対して垂直に立ちます。
Aさんが水平の方向に対して先端Pを見上げる角度が15になる位置に、Bさんが2点A、Qを結んだ線分上で、水平の方向に対して先端Pを見上げる角度が30になる位置に立ち、次の長さがわかると、鉄塔の高さPQを求めることができます。
2人の目の高さAAとBBが等しく、AAが1.5m、AさんとBさんの間の距離ABが50mであるとき、鉄塔の高さPQは【ア】mになります。