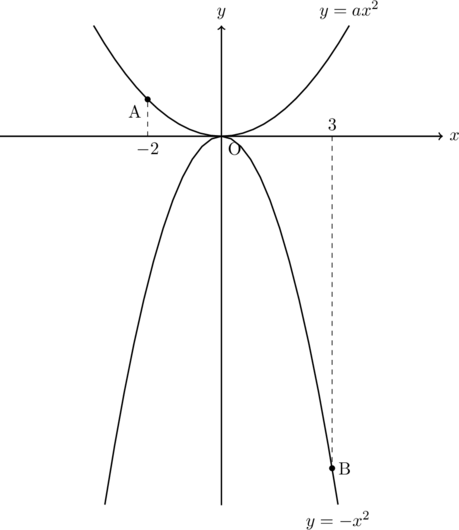
こんにちは。相城です。今回は2020年3月2日に行われました千葉県の後期入試から放物線の問題をピックアプしました。それではどうぞ。
下の図のように、関数![]() のグラフと、関数
のグラフと、関数![]() のグラフがある。関数
のグラフがある。関数![]() のグラフ上に
のグラフ上に![]() 座標が
座標が![]() の点Aがあり、関数
の点Aがあり、関数![]() のグラフ上に
のグラフ上に![]() 座標が3の点Bがある。点Aの
座標が3の点Bがある。点Aの![]() 座標が、点Bの
座標が、点Bの![]() 座標より10大きいとき、次の(1)、(2)の問いに答えなさい。
座標より10大きいとき、次の(1)、(2)の問いに答えなさい。
ただし、![]() とする。
とする。
また、原点Oから点(1, 0)までの距離及び原点Oから点(0, 1)までの距離をそれぞれ1㎝とする。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) 2点A、Bを通る直線と、![]() 軸との交点をCとする。
軸との交点をCとする。
このとき、次の①、②の問いに答えなさい。
① 点Cの![]() 座標を求めなさい。
座標を求めなさい。
② △OACを、![]() 軸を軸として1回転させてできる立体の体積を求めなさい。
軸を軸として1回転させてできる立体の体積を求めなさい。
ただし、円周率は![]() を用いることとする。
を用いることとする。

答え
(1)
B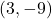 であるから、Aの
であるから、Aの 座標は
座標は 。つまりA
。つまりA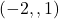 である。ゆえに
である。ゆえに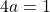 となり、
となり、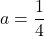
(2)
① A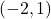 、B
、B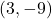 、Bの座標から
、Bの座標から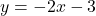
Cの 座標は0なので、
座標は0なので、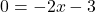 とすると、
とすると、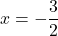
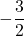
②
B
(2)
① A
Cの
②

![]() 軸を中心に△PQAを1回転させてできる立体(円錐A)から、△POCを1回転してできる立体(円錐B)と、△OQAを1回転させてできる立体(円錐C)をひいて求めます。
軸を中心に△PQAを1回転させてできる立体(円錐A)から、△POCを1回転してできる立体(円錐B)と、△OQAを1回転させてできる立体(円錐C)をひいて求めます。
円錐A=![]()
円錐B=![]()
円錐C=![]()
よって求める体積は
![]()
![]() cm
cm![]()
 数樂管理人のブログ
数樂管理人のブログ 


間違えました 4分の3πですよね?
解答はこちら
大問3になります。
https://www.school-data.com/exam_archives/exam_result/2020/pdf_data/chiba_k_sugaku.pdf
ご確認よろしくお願いします。