こんにちは。相城です。円周率が3より大きいことは中学生(中学生で三平方の定理を履修済みなら)でも証明可能ということを示しておきます。円周率が3.05より大きいことを証明せよは, 東京大学で出題された有名な問題でもあります。それではどうぞ。
正方形に内接する円と正多角形
円の面積は(半径)![]() (半径)
(半径)![]() (円周率)で与えられる(証明略)。
(円周率)で与えられる(証明略)。
一辺が20の正方形に内接する円を考える。その円に内接する正多角形を考え,
右の図は正八角形の場合である。正八角形を円の中心Oを中心に合同な三角形に八等分してみる。
このときできる三角形は頂角45![]() , 頂角をはさむ2辺は10の二等辺三角形になる。
, 頂角をはさむ2辺は10の二等辺三角形になる。
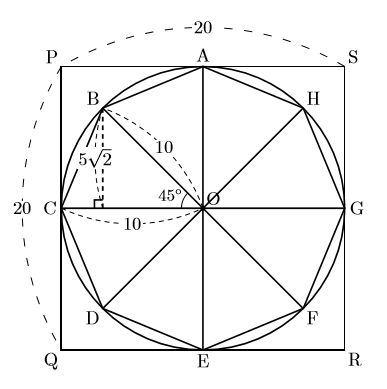
ここで△OBCについて面積を求める。
点Bから辺OCに下ろした垂線の長さは![]() (三平方の定理,
(三平方の定理, ![]() )であるから, △OBCの面積
)であるから, △OBCの面積![]() は,
は,
![]()
正八角形の面積は
![]()
またこのとき正方形の面積を
![]()
正方形の面積は400, 円の面積を,
![]()
両辺100で割ると,
![]()
となり円周率はこの範囲にあることがわかる。
右の図は正十二角形の場合である。正十二角形を円の中心Oを中心に合同な三角形に十二等分してみる。
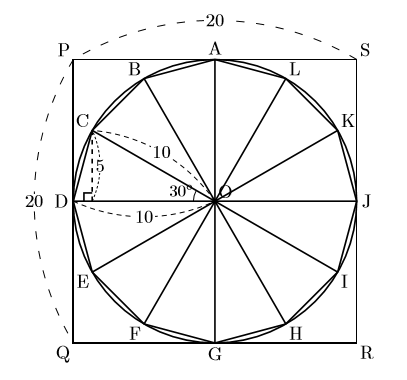
このときできる三角形は頂角30![]() , 頂角をはさむ2辺は10の二等辺三角形になる。ここで△OCDについて面積を求める。
, 頂角をはさむ2辺は10の二等辺三角形になる。ここで△OCDについて面積を求める。
点Cから辺ODに下ろした垂線の長さは5(三平方の定理, ![]() )であるから, △OCDの面積
)であるから, △OCDの面積![]() は,
は,
![]()
正十二角形の面積は
![]()
同様に, 正方形の面積と円の面積の関係を示すと,
![]()
両辺100で割ると,
![]()
となり円周率はこの範囲にあることがわかる。
このことから円周率
正360角形ならどうなの?
最後に高校生になったら習う技を使って, 正360角形の面積を電卓を使って求めてみます。
長さや設定は先ほどと同じです。
下の図のような, 三角形の面積![]() は,
は,
![]()
で与えられる。
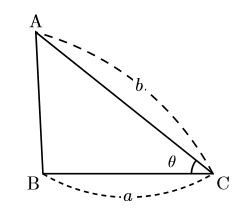
これが高校生で習う技である。ちなみにこれは底辺![]() 高さ
高さ![]() 2の 基本公式の形を変えただけであるが, 本題から外れるのでここでは紹介だけにしておく。
2の 基本公式の形を変えただけであるが, 本題から外れるのでここでは紹介だけにしておく。
求める三角形の面積は, 頂角(ここでは![]() )1
)1![]() ,
, ![]() の三角形であるから, その面積
の三角形であるから, その面積![]() は,
は,
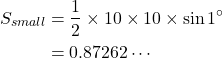
となる。
これが360個集まったのが, 正360角形なので, この面積
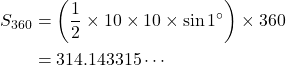
となり, 先と同様に比較すると,
![]()
となる。
正
お気づきの人もいたかもしれませんが, 今回正多角形は円に内接していますが, 外接する場合も考えて, ![]() の値を絞り込んでも面白いでしょう。また, 周の長さで考えると, 正六角形のとき円周率3になるのですかね? この矛盾が僕には分かりません。まだまだ修行不足です。それではまた。
の値を絞り込んでも面白いでしょう。また, 周の長さで考えると, 正六角形のとき円周率3になるのですかね? この矛盾が僕には分かりません。まだまだ修行不足です。それではまた。
 数樂管理人のブログ
数樂管理人のブログ 

