こんにちは。相城です。今回は, 題は連立方程式とありますが, 文章問題の攻略です。それではどうぞ。
連立方程式の文章題の攻略
文章の捉え方(読み方)
句読点( , 。 )で区切って読む。
(基本問題なら 。までの一つの文で必ず1つまたは2つの式ができる。)ただし一番初めの ( , 。)の一文は状態(どんな場面か)を表していることが多い。
下の基本パターンの①で求めたいものとは文章問題の最後に出てくるのがほとんどである。
攻略法の基本パターン
- 文をよく読んで, 求めたいものは何か調べる。
- 求めたいものを
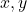 とおく。
とおく。 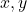 に関する式を2つ作る。
に関する式を2つ作る。- 解く。
- 答えが問題にあっているか考える。
- 必要なら単位などを付けて答えを書く。
(注)基本問題でも求めたいものを![]() とおかない場合がある。
とおかない場合がある。
それはその都度勉強していけばよい。
基本的に式は日本語通りにつくる
- 兄は弟より3000円多い。(兄
- 兄は→
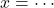 (は, が, はイコール(
(は, が, はイコール(  )と同じ意味)
)と同じ意味) - 弟より3000円多い→
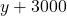 (
(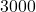 円多いので
円多いので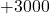 円,少なければ
円,少なければ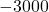 円)
円) - は, が(英語で言うbe動詞)→イコールで結べ
入試問題の特徴は, 1つ目の式は簡単にできることが多いです。ただ, 2つ目の式をつくるのがややこしいことが多いです。
文章をよく読まないとできなかったり, つくった後, 整理(計算)するのに時間がかかったり様々です。
ですから, 家庭学習では2つ目の式への意識を心がけて, 問題に取り組んでください。
例題を見ていこう
ある店で,50円切手と80円切手を合わせて20枚買ったら,
代金の合計は1360円であった。
このとき50円切手と80円切手をそれぞれ何枚買ったか求めなさい。
読み方
- 読み方
- ある店で,
 どんな店かの情報
どんな店かの情報 - 50円切手と80円切手を合わせて20枚買ったら,
 2つの枚数を合わせると20枚
2つの枚数を合わせると20枚 1つ目の式
1つ目の式 - 代金の合計は1360円であった。
 2つの代金の合計が1360円
2つの代金の合計が1360円 2つ目の式
2つ目の式 - このとき50円切手と80円切手をそれぞれ何枚買ったか求めなさい。
 求めたいもの,
求めたいもの, 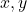 とおくもの
とおくもの
解法
50円切手の枚数を![]() 枚, 80円切手の枚数を
枚, 80円切手の枚数を![]() 枚とおくと,
枚とおくと,
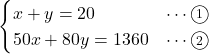
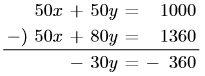
![]()
![]() を
を![]() に代入して,
に代入して,
![]()
![]() は問題にあっている。
は問題にあっている。
よって,
50円切手8枚,80円切手12枚・・・(答)
14km離れた2地点A,Bがある。A地点を出発して時速3kmの速さで進み, 途中から時速5kmで進んだところ, B地点に着くまでに4時間かかった。時速3kmで進んだ道のりと時速5kmで進んだ道のりを求めなさい。
読み方
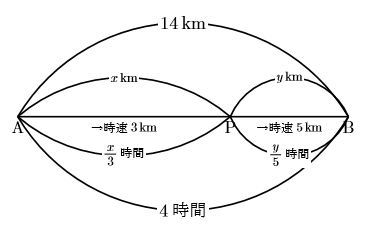
- 読み方(道のり
- 14km離れた2地点A, Bがある。
 AとBは14km離れている。
AとBは14km離れている。 1つ目の式
1つ目の式 - A地点を出発して時速3kmの速さで進み,
 時速3kmで進んだ道のりがある。
時速3kmで進んだ道のりがある。 km
km - 途中から時速5kmで進んだところ,
 時速5kmで進んだ道のりがある。
時速5kmで進んだ道のりがある。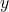 km
km - B地点に着くまでに4時間かかった。
 A地点からB地点まで合計4時間かかった。
A地点からB地点まで合計4時間かかった。 2つ目の式
2つ目の式 - 時速3kmで進んだ道のりと時速5kmで進んだ道のりを求めなさい。
 求めたいもの
求めたいもの ,
,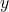 とおくもの
とおくもの
解法
時速3kmで進んだ道のりを![]() km, 時速5kmで進んだ道のりを
km, 時速5kmで進んだ道のりを![]() kmとおくと,
kmとおくと,
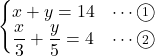
時速3kmで進んだ道のりは9km, 時速5kmで進んだ道のりは5km・・・(答)
例題 ある中学校の生徒全員が, 〇か×どちらかで答える1つの質問に回答し, 58![]() が〇と 答えた。また, 男女別に調べたところ, 〇と答えたのは男子で70
が〇と 答えた。また, 男女別に調べたところ, 〇と答えたのは男子で70![]() , 女子では45
, 女子では45![]() であり, 〇と答えた人数は, 男子が女子より37人多かった。 この中学校の男子と女子の生徒数をそれぞれ求めなさい。【福島】
であり, 〇と答えた人数は, 男子が女子より37人多かった。 この中学校の男子と女子の生徒数をそれぞれ求めなさい。【福島】
読み方
- これを解読し, 連立方程式をつくろう。
- ある中学校の生徒全員が, 〇か×のどちらかで答える1つの質問に回答し, 58
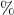 が〇と答えた。
が〇と答えた。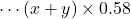 (人)
(人) - また,男女別に調べたところ,
 と答えたのは男子で70
と答えたのは男子で70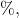 女子では45
女子では45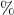 で あり,
で あり,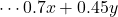 (人)
(人) - ○と答えた人数は,男子(
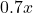 (人))が(
(人))が( )女子より37人多かった(
)女子より37人多かった(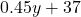 (人))。
(人))。
求めたい男子と女子の人数をそれぞれ
①と②ともに, 〇を付けた生徒の合計人数を表しています。ですから①![]() ②が成り立ちます。
②が成り立ちます。
それと最後の行で, 男子女子の人数関係で1つ式ができます。
それが以下の連立方程式です。
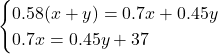
このようにして, 比較的取り組みやすい文章問題を解き, 文章に慣れていくことが, それ以上の問題を解くコツにつながっていきます。
負けずに頑張ってください。
 数樂管理人のブログ
数樂管理人のブログ 

