こんにちは。今回は等式の変形についてです。攻め方を書いてみました。
等式変形・中1で習った方程式
等式の変形って実は中学1年生でやってるんですね。
中学1年生の等式で, 代表的なものが, 方程式です。
例えば
次の方程式を解け
![]()
というものがあったとします。
これを解いていくと, 左辺の
![]()
![]()
両辺3でわって,
![]()
となります。このようにある等式から,
中学校2年生では, 解く文字が
等式の性質
本題に入る前に, 等式の性質を復習しましょう。
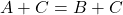
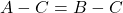
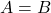
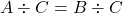 (但し,
(但し, 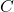 は0でない。)
は0でない。)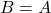
この等式の性質の言わんとするところは, 結局等式の変形というのは, 方程式と同じように移項ができ, 両辺に何を掛けてもいいし, 0以外の数字であれば両辺を何で割ってもいいということです。
例題を見ていこう
では例題を見ていきましょう。
問題では, ![]()
![]() の中の文字について解きなさいと出てきます。
の中の文字について解きなさいと出てきます。
この意味を例題を見ながら解いていきましょう。
例題![]()
![]() の中の文字について解きなさい。
の中の文字について解きなさい。
例題①
![]()
まず,
左辺にある
![]()
これで,
よって, 答えは
![]()
例題②
![]()
まず,
左辺にある
![]()
一番最初にした方程式では, 右辺は計算できたけど, ここでは計算できません。したがって,
にするためには, 両辺を3で割ってやる。
よって, 答えは
![]()
例題③
まず, ![]() について解く→
について解く→ ![]() ~に変形することなので,
~に変形することなので,
右辺と左辺を入れ換えて,
![]()
両辺2倍して, 整数の形にして,
![]()
両辺
![]()
例題④
![]()
まず,
右辺と左辺を入れ換えて,
![]()
かっこをはずして,
![]()
8
![]()
両辺
![]()
解くときのコツ
最後数字(特にマイナスの数字)で割るときは1つずつ割っていった方が, 符号ミスとか少なくなるので, その方がいいと思う。
また, その方が後の単元の一次関数を習うときに, しっくりくると思う。まとめて割り算する方法は効率的ではあるが, 慣れないと使い分けが難しい。
例題④の別解
例題④でかっこをはずすところは,
かっこをはずさなくてもできる。 ただ, 日ごろから慣れているかっこをはずすという方法で行った方がしっくりくると思うので, そちらの解法を選んだ。最後に別解として, かっこをはずさない方法を以下に記しておく。
例題④の別解
![]()
右辺と左辺を入れ換えて,
![]()
両辺4で割って,
![]()
![]()
両辺
![]()
 数樂管理人のブログ
数樂管理人のブログ 

