中学数学：攻略・三角形の合同

こんにちは。相城です。今回は三角形の合同の証明の攻略法を見ていきましょう。動画でご覧になりたい方は下部に載せていますのでご覧ください。それではどうぞ。

三角形の合同の証明の攻略

三角形の合同の証明の基本の流れ

文をよく読んで, 仮定と結論を区別する。
仮定からわかることを図形にチェック。
合同な三角形を1組み選ぶ。
仮定から等しい数量を2つ書く。
定理や図形の性質から等しいものを1つ書く。
合同条件。
結論。

※問題文の中から, 合同条件を満たすための3つのうち最低2つはわかる。

上記は, ほとんどのパターンで使える。
図形が苦手, でも得意になりたい人は①の仮定と結論の区別の練習をし,
その中でも合同な図形に必要なものを選ぶ練習をするとよい。

例題を見ていきましょう

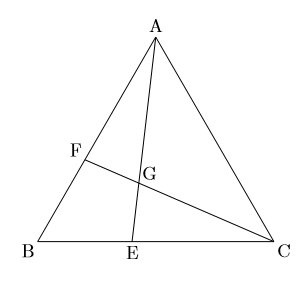
例題下の図で, △ABCは正三角形, 辺AB, 辺BC上にAF $=$ CEとなる点F, Eをとる。また, 線分AEと線分CFの交点をGとする。このとき, △ABE $\equiv$ △CBFであることを証明しなさい。

仮定
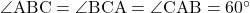$\angle{\text{ABC}}=\angle{\text{BCA}}=\angle{\text{CAB}}=60^{\circ}$ , AB $=$ BC $=$ CA, AF $=$ CE
結論
△ABE $\equiv$ △CBF

解答例

証明
△ABEと△CBFで,
仮定より
AB $=$ CB $\cdots\textcircled{\scriptsize 1}$
$\angle{\text{ABE}}=\angle{\text{CBF}}=60^{\circ}\cdots\textcircled{\scriptsize 2}$
AF $=$ CE, AB $=$ BCより,
BE $=$ BF $\cdots\textcircled{\scriptsize 3}$
$\textcircled{\scriptsize 1}$ , $\textcircled{\scriptsize 2}$ , $\textcircled{\scriptsize 3}$ より,
2組の辺とその間の角がそれぞれ等しいので,
△ABE $\equiv$ △CBF

上の証明で, $\textcircled{\scriptsize 1}$ , $\textcircled{\scriptsize 2}$ は仮定より分かっている。ここで証明したい△ABE, △CBFで1つの辺と1つの角が分かっている。ということは, 合同条件と照らし合わせた場合, あと1つ知りたいのは1組の辺とその両端～, か2組の辺とその間の～どちらかに絞れる。どちらかに
なるはずなので, じっくり図形を見て性質などから証明できる方を導く。これが $\textcircled{\scriptsize 3}$ である。
ちなみに $\textcircled{\scriptsize 2}$ のように角度が分かるものは書いてやるのが礼儀。

プリントアウト用pdf

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル