中学数学：攻略・多面体の辺や頂点のからくり

こんにちは。相城です。今回は正多面体のとらえ方です。普通の多面体にも使えるので, 押さえておいてください。

多面体はこう考えてみよう

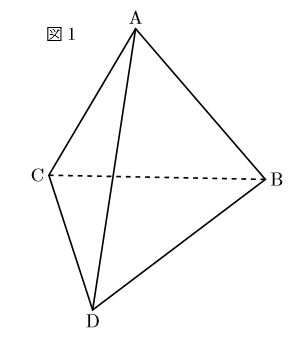
図1は正四面体の見取り図です。辺の数や頂点の数を求めるのはそんなに苦ではないでしょう。 見て数えられるし, その方が早いかもしれません。ここでは立体の辺の数や頂点の数の数え方について, 少し触れてみましょう。
まず, 正多面体とはすべての面が合同な正多角形でできており, どの頂点にも集まる面の数が同じの立体です。 定義はこんな感じですが, どの頂点に集まる辺の数も実は同じだったりします。まぁそんなことはさておき, 図1は正四面体で, 合同な正三角形が4つあります。正三角形は辺の数が3本, 頂点が3つ ですから, 全部で辺の数は
(本)
同じく頂点の数は
(個)
あります。
ここで1本の辺を作るのに必要な三角形は2枚ですから, 実際に合同な正三角形を4つ使ってできる辺の数は
(本)
1つの頂点に集まる面の数は3つですから, 実際に組み立ててできる頂点の個数は
(個)
となります。

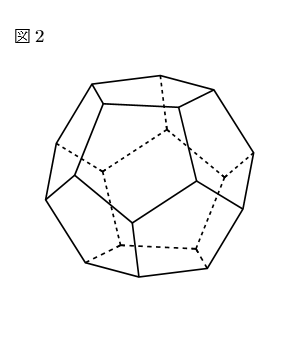
図2は正十二面体です。面はすべて合同な正五角形からできており, 先ほどと同じ考え方でいけば, 正五角形の辺の数, 頂点の数はともに5つで,
全部で辺の数は
(本)
頂点の数は
(個)
あります。
しかし, 実際辺を作るのに必要な面の数は2つなので, 実際組み立ててできる辺の数は
(本)
1つの頂点を作るのに必要な 面の数は図2より3つなので, 実際にできる頂点の数は
(個)
となります。
この考え方は正多面体だけでなく, いろいろな立体に応用が利くので是非マスターしておきたいですね。
また、オイラーという偉い人が発見した多面体の定理を紹介しておきます。
(頂点の個数)＋(面の数)－(辺の数)

プリントアウト用pdf