こんにちは。相城です。今回は因数分解の攻略を見ていきましょう。
因数分解とは
因数分解は展開の逆の作業のことをいいます。
全てではありませんが, 簡単に言うと, かっこの無い式をかっこのある式に変形します。難しい言い方をすれば和の形を積の形だけに変換する作業です。
中2で習った因数分解
因数分解って, 厳密には中3で習うんですが, 中2で実はすこしかじっているんです。偶数![]() 偶数は偶数っていう文字式の説明ってやったでしょ?覚えていますか?2つの偶数を
偶数は偶数っていう文字式の説明ってやったでしょ?覚えていますか?2つの偶数を![]() ,
, ![]() とすると, その和を求めると,
とすると, その和を求めると,
![]()
この作業を因数分解って言うんですね。
左辺の
このように, 共通する文字や数字を最大限とりだすことを因数分解といいます。
この共通する因数のことをそのまま共通因数といいます。
因数分解の基本思考の4パターン
基本1
因数分解では, 共通因数を取り出すことが基本となります。
![]()
ここで,
因数とは約数のことであることは, 素因数分解のところで勉強しました。こうやって, 式も因数で分解していきます。
基本2
現行教科書では公式から因数分解をたどっていますが, 今回は因数分解の本質?的なところから入っていきます。
それは, 展開すると
![]()
なるのであれば,
![]()
と因数分解できるということです。
ではどうやって考えるか, それは数字に隠されています。6という数字は最後ある2つの数を掛け算して得られた数です。また, 5はある2つの数を足して 得られた数ということは公式から分かることです。ここで, 掛け算して6になる2数を考えた方が有効か, 足して5になる2数を考えた方が有効かを考えた場合, 整数の範囲に限定しても, 足して5になる2数の組み合わせは無限にあることに気付くでしょう。そして掛けて6になる2数の組み合わせ方が有限個です。ですから, 掛けて6になる2数を考えていきます。
掛けて6になる数も考え方によっては無限にありますが, 中学校の因数分解は基本的には整数の範囲で行うことが多いので, それはイレギュラーな例としてここでは扱わないことにします。
では掛けて6になる組み合わせを考えると, 以下の表ができます。

この表から, 掛けて6足して5になる2数の組み合わせは2と3になります。したがって, ![]() は
は![]() と因数分解できるのです。
と因数分解できるのです。
基本3
残りの公式もこれが基本で因数分解できます。
例えば, ![]() の因数分解も, いまやったやり方で解けます。
の因数分解も, いまやったやり方で解けます。
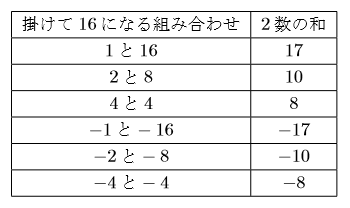
この表から, 足して![]() になる組み合わせは
になる組み合わせは![]() と
と![]() になります。したがって,
になります。したがって,
![]() となり, 同じ式は累乗を使って書くので,
となり, 同じ式は累乗を使って書くので, ![]() と因数分解できます。
と因数分解できます。
基本4
次に, ![]() の因数分解も同様に考えることができます。
の因数分解も同様に考えることができます。
今度は掛けて![]() , 足して0になる組み合わせを考えればいいので,
, 足して0になる組み合わせを考えればいいので,

この表から, 掛けて![]() , 足して0の組み合わせは4と
, 足して0の組み合わせは4と![]() である。したがって,
である。したがって,
![]() は
は![]() と因数分解できます。
と因数分解できます。
この4パターンが基本になります。
あとはこれらを組み合わせたりしているだけです。
応用例題
少し応用問題をいくつかやって終わりたいと思います。
(1) ![]() を因数分解しなさい。
を因数分解しなさい。
(2) ![]() を因数分解しなさい。
を因数分解しなさい。
(3) ![]() を因数分解しなさい。
を因数分解しなさい。

(1) 共通因数![]() でくくって, さらに因数分解
でくくって, さらに因数分解![]() ・・・(答)
・・・(答)
(2) ![]() とおくと
とおくと![]() , これを因数分解すると,
, これを因数分解すると,![]()
![]() として計算すると,
として計算すると,![]() ・・・(答)
・・・(答)
(3) ![]() とおくと
とおくと![]() , 共通因数
, 共通因数![]() でくくると,
でくくると,![]() ,
, ![]() にもどすと,
にもどすと,![]() ・・・(答)
・・・(答)
 数樂管理人のブログ
数樂管理人のブログ 

