こんにちは。相城です。今回は平方根を見ていきましょう。
平方根って何?
さていよいよ?数学らしくなってくるときが来ました。無理数(むりすう)というものをこれから学びます。 無理数については簡単に触れる程度の説明として, 新しい数学の記号と概念をここでは学んでください。
2乗してある数![]() になる数を考えていくことにします。
になる数を考えていくことにします。
例えば, 2乗して36になる数は, なんですか?
![]() と
と![]() です。
です。
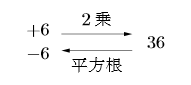
そうですね。このとき, この2つの数(![]() プラスマイナス6と読む)を36の平方根といいます。このとき,
プラスマイナス6と読む)を36の平方根といいます。このとき,
![]() は
は![]() の正の平方根
の正の平方根
![]() は
は![]() の負の平方根
の負の平方根
となります。
2乗すると![]() になる値を
になる値を![]() の平方根といいます。
の平方根といいます。
この場合, 36の平方根は![]() ということです。
ということです。
一般に, ある数![]() の平方根は, 次の関係を満たす
の平方根は, 次の関係を満たす![]() になります。
になります。
![]()
ですから, 平方根は正と負の2つあることになります。
ただ, 0の平方根は0しかありません。
つまり,
64の平方根は8と![]() (
(![]() )
)![]() の平方根は
の平方根は![]()
0.04の平方根は![]()
となります。
2乗して負になる数は中学校では学びません。
では, 上に書いたようにすんなり求まる数字はいいでしょう。考えなくてはいけないのが平方根がきちんと求まらない数です。
どういった数かといいますと, 例えば2という数字。
2乗して2になる数はいくつなんでしょうか。
![]()
![]()
このことから, 2乗して2になる数は1.41と1.42の間にあります。
このことから, 2乗して2になる数は1.414と1.415の間にあることが分かります。以下ずっと計算していけば,
2乗して2になる数を突き詰めていくことができます。
ただ, それは永遠に行っていかなくてはいけない作業になります。
このように, ある数の平方根が特定の数字として求まらないときは記号![]() (記号の名は根号)を使って平方根を表すのが約束です。
(記号の名は根号)を使って平方根を表すのが約束です。
したがって,
2の平方根は![]() (
(![]() ルート2と読む)
ルート2と読む)
となります。
このように![]() を使って表した数字を無理数といいます。
を使って表した数字を無理数といいます。
一般に, ある数![]() の平方根は
の平方根は![]() となります。
となります。
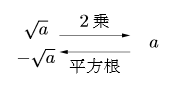
平方根![]() は二乗するとある数
は二乗するとある数![]() になりますが,
になりますが,
![]() の中がある数の2乗になるときは
の中がある数の2乗になるときは![]() がはずれます。
がはずれます。
例えば, 25の平方根は![]() ですが,
ですが, ![]() であるから,
であるから, ![]() となって, 2乗すると25になる数がきちんと存在します。その場合は,
となって, 2乗すると25になる数がきちんと存在します。その場合は, ![]() とは書かず,
とは書かず, ![]() となります。 ですから何でもかんでも
となります。 ですから何でもかんでも![]() を付ければいいというものではありません。
を付ければいいというものではありません。
問題
ここで簡単な?問題(解答はこのページの最後に掲載)
Q1~Q5の文を読んで, 下線部の誤りがあるものは訂正しなさい。
Q1. ![]() は
は![]() である。
である。
Q2. 10の平方根は![]() である。
である。
Q3. ![]() の平方根は
の平方根は![]() である。
である。
Q4. ![]() である。
である。
Q5. ![]() の平方根は
の平方根は![]() である。
である。
平方根の大小
平方根の大小
平方根もれっきとした数ですから大小関係が存在します。![]() を正の数とし,
を正の数とし, ![]() であるとするなら,
であるとするなら,
![]()
という関係が成り立ちます。
例
![]()
例
![]()
例
![]()
このように正の数, 負の数と同様に大小関係が示すことができます。
余談
以下余力のある人。中学生レベルではほとんどいらない知識ですので,
余談ですが平方根の平方とは2乗と同じ意味です。面積の単位でcm![]() 平方センチメートルって言いますよね。 2乗があるのなら3乗, 4乗,
平方センチメートルって言いますよね。 2乗があるのなら3乗, 4乗, ![]() ってありますから, 平方根の次に3乗根(立方根), 3乗根の次に4乗根,
ってありますから, 平方根の次に3乗根(立方根), 3乗根の次に4乗根, ![]() ってありそうですね。8の3乗根は2です。2を3乗すれば8になりますよね。
ってありそうですね。8の3乗根は2です。2を3乗すれば8になりますよね。 ![]() の3乗根は
の3乗根は![]() , 2の3乗根はきちんと求まらないので,
, 2の3乗根はきちんと求まらないので, ![]() と書きます。
と書きます。
Q1~Q5の答え
Q1. ![]() は
は![]() である。
である。
正しい。
Q2. 10の平方根は![]() である。
である。
![]()
Q3. ![]() の平方根は
の平方根は![]() である。
である。
36
Q4. ![]() である。
である。
5
Q5. ![]() の平方根は
の平方根は![]() である。
である。
![]()
 数樂管理人のブログ
数樂管理人のブログ 

