中学数学：攻略・グラフ問題の入り口

こんにちは。相城です。グラフ問題もこうやって考えたらいいかも。また, こうやって解いていくといいかもってことをお話しできればと思います。それではどうぞ。

グラフ問題の捉え方

一次関数のグラフの式は目で見て求める。

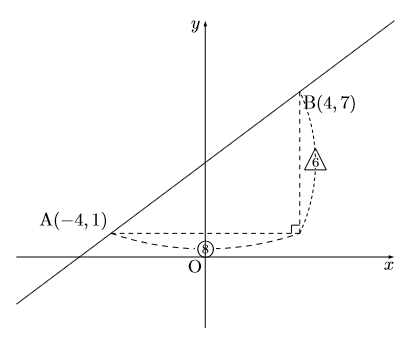
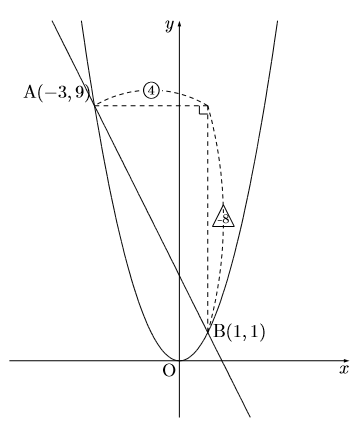
個人的感想ですが, グラグが問題用紙に書いてあり 2点の座標が分かるときは, その2点を斜辺とする 直角三角形を作って直線の傾きを求めたほうが早い。 ただ, 苦手な生徒は2点の座標を連立方程式を使って 直線の式を求める作業をすることをお勧めします。 勿論を使ってもよし, その他の公式を使ってくれてもよい。この直角三角形こそ、を求める作業であり, それがグラフの傾きになっている。図のがxの増加量, がyの増加量である。従って図1の直線の傾きは,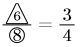
図2直線の傾きは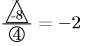である。
ただ, グラフは常に右側に見る、つまり軸の正の方向を基準に見たほうが良いのでその辺り気を使ってください。
個人的に軸の負の方向に見るのは好きではないので。

求められるものは先に求めておく

問題で使う使わないは別として、分かる座標は全て問題用紙に書き込んでおく。

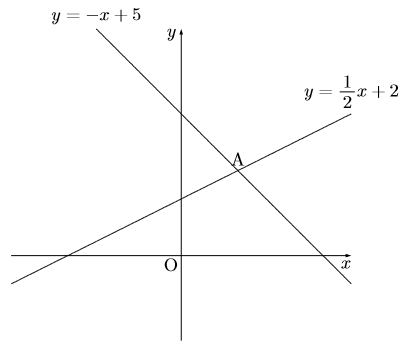
右の図のように直線は点Aで直線と交わる。このとき次の問いに答えなさい。
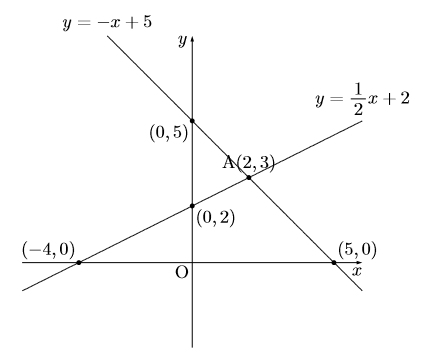
このような問題があった場合とりあえず分かる座標は全て求めておくのがよいと考える。それから 問題を解いても余裕があるぐらいのスピードをつけたいものです。それではまた。

プリントアウト用pdf