こんにちは。相城です。今回はグラフと三角形について簡単に触れたいです。後半部分は等積変形使ったりしてますが。考え方の例として受け止めてくださればと思います。それではどうぞ。
三角形の面積の問題(![]() 軸,
軸, ![]() 軸に平行な辺があるとき。)
軸に平行な辺があるとき。)
例題1
関数![]() ,
, ![]() が点Aで交わっている。
が点Aで交わっている。
また![]() 軸に平行で
軸に平行で![]() 座標が
座標が![]() の直線と2つのグラフの交点をP, Qとするとき,
の直線と2つのグラフの交点をP, Qとするとき,
△APQの面積を求めなさい。
考え方
この手の問題は![]() 軸,
軸, ![]() 軸に平行な直線がある場合は, それを底辺として考えると, 片付く問題がほぼ100
軸に平行な直線がある場合は, それを底辺として考えると, 片付く問題がほぼ100![]() になります。この場合線分PQが
になります。この場合線分PQが![]() 軸に平行なので, 線分PQを底辺とすれば三角形の面積は簡単に求まります。
軸に平行なので, 線分PQを底辺とすれば三角形の面積は簡単に求まります。

![]() 軸,
軸, ![]() 軸に平行な直線がある場合は, それを底辺として考える
軸に平行な直線がある場合は, それを底辺として考える
次に, 三角形の底辺と思われるものが, ![]() 軸,
軸, ![]() 軸に対して斜めになっている場合は, その三角形が, ちょうど入る長方形を作り余分な三角形を引けば求まる。しかし, ここでは二次関数を例に公式的なもので求めてみます。
軸に対して斜めになっている場合は, その三角形が, ちょうど入る長方形を作り余分な三角形を引けば求まる。しかし, ここでは二次関数を例に公式的なもので求めてみます。
例題2
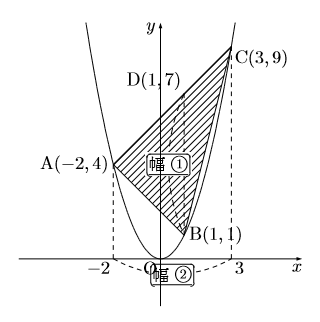
右の図は![]() のグラフで, そのグラフ上に3点A(
のグラフで, そのグラフ上に3点A(![]() ), B(1, 1), C(3, 9)をとったものです。このとき, △ABCの面積を求めなさい。
), B(1, 1), C(3, 9)をとったものです。このとき, △ABCの面積を求めなさい。
考え方
このとき直線ABの式(![]() )を求めて, 点Bから
)を求めて, 点Bから![]() 軸に平行な直線と直線ABとの交点をDとするとD(1, 7)となり, 幅①
軸に平行な直線と直線ABとの交点をDとするとD(1, 7)となり, 幅①![]() 幅②
幅②![]() 2で求まる。もちろん, 幅①を底辺として, 左右2つの三角形の面積を別々に求めて最後に足してもよい。
2で求まる。もちろん, 幅①を底辺として, 左右2つの三角形の面積を別々に求めて最後に足してもよい。
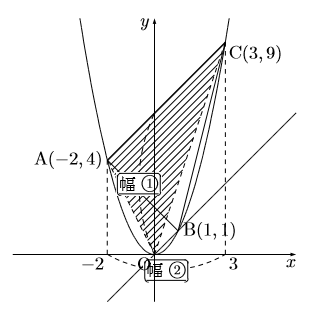
また, もう1つの解法は, 等積変形です。直線ABの傾きを求め, 直線ABに平行で点Bを通る直線を求める(この場合![]() )。この直線と
)。この直線と![]() 軸との交点(この場合原点)を求めて, 先と同様に幅①
軸との交点(この場合原点)を求めて, 先と同様に幅①![]() 幅②
幅②![]() 2で求めてもよい。
2で求めてもよい。
さらに, もう1つ等積変形ですが, ![]() 軸または
軸または![]() 軸に平行に頂点を動かしてやることも可能である。
軸に平行に頂点を動かしてやることも可能である。
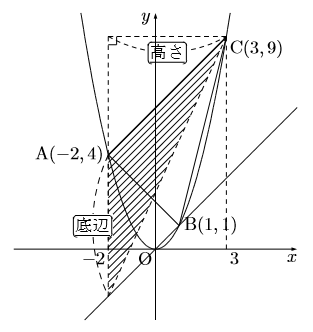
等積変形はどの頂点を動かせば効率が良いか, という観点から見るとよい。特に直線の式の傾きが知れる場合は, それに平行な直線で考えてみるのもよい。
![]() 軸,
軸, ![]() 軸に平行な直線がない場合は, 幅①
軸に平行な直線がない場合は, 幅①![]() 幅②
幅②![]() 2, 幅①で2つの三角形に分ける。等積変形などを使おう。
2, 幅①で2つの三角形に分ける。等積変形などを使おう。
あと原点が1つの頂点である場合, 2つの座標をたすきがけしたものの差の絶対値の![]() で求められます。紹介だけしておきます。
で求められます。紹介だけしておきます。
3点![]() ,
, ![]() ,
, ![]() を頂点とする三角形の面積
を頂点とする三角形の面積![]()
![]()
![]() は絶対値の記号(例:
は絶対値の記号(例:![]() )
)
どの3点も原点にない場合は, 3点のどれか1つを基準にして, 原点に平行移動させて考えるとうまくいく。
 数樂管理人のブログ
数樂管理人のブログ 

