中学数学：攻略法：関数と図形(三角形の等積変形)

こんにちは。相城です。今回は関数と図形の中で, 三角形の面積と等しい三角形をつくる問題を攻略してみたいと思います。

例題を見てみよう

右の図で, 直線 $\ell$ は, $y=\dfrac{2}{3}x+5$ , 直線 $m$ は $y=-4x+5$ , 直線 $n$ は $y=-\dfrac{1}{2}x-2$ である。
直線 $\ell, m$ , 直線 $\ell, n$ , 直線 $m, n$ の交点をそれぞれA, B, Cとする。このとき, $x$ 軸上の正の部分の点で, △ABC $=$ △ABPとなる点Pの座標を求めなさい。

ポイントはアルファベットにあり

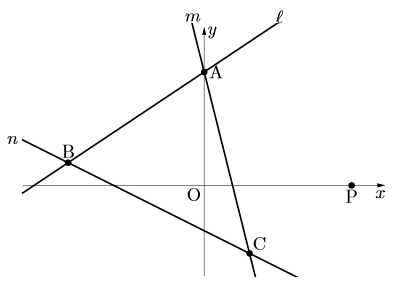
このような問題が, よく出題されると思うが, ポイントは問題文にある△ABC $=$ △ABPである。結論から言うとアルファベットなのである。2つの三角形に共通なアルファベットが2つあるでしょ。AとB, これは求める過程で動かない点なのである。このABが, 間違いなく定辺(動かない辺)になる。三角形の面積の等積変形は, 必ずと言っていいほど, 1つの頂点を動かすものある。したがって, 共通な2つのアルファベットを結ぶ線分は定辺になり, その線分(定辺)に対して, 残りの頂点(3つ目の頂点)を通るように平行線を引けばよいのである。つまり今回は, 線分AB(定辺)に平行な直線で, 残りの頂点である点Cを通る直線を求め, $x$ 軸との交点を求めるとよいのである。
これが, この手の問題を解くポイントである。
ちなみに今回は, 傾き $\dfrac23$ で点C( $2, -3$ )を通ることから, 求める直線は
$y=\dfrac{2}{3}x-\dfrac{13}{3}$ となる。
$y=0$ とおいて, $x=\dfrac{13}{2}$ よって, P $\left(\dfrac{13}{2}, 0\right)$