中学数学：攻略・関数と図形(正方形になる)

こんにちは。相城です。今回は関数と図形の中でも頻出になる正方形になるときの云々の問題の攻略法を見ていきましょう。下部に中3生の放物線の問題の動画を載せています。それではどうぞ。

縦の長さ＝横の長さと式をつくる

関数と図形問題で正方形になるときの座標云々の攻略法は一言で言えば,

攻略法

(縦の長さ) $=$ (横の長さ)の式をつくる

これでほぼ解ける。
ただ座標を文字で置かなければならないのがほとんどなので,
日頃から座標を文字で表すことに慣れておく必要がある。

例題を見ていきましょう

【例題】関数 $y=2x^2$ (下のグラフの内側) , $y=x^2$ (下のグラフの外側)があり, $y=x^2$ のグラフ上に点Aをとり, 点Aを通り $y$ 軸に平行な直線と $y=2x^2$ のグラフの交点をBとする。このとき, ABを1辺とする正方形ABCDをつくる。点C, Dが $y$ 軸上にあるとき点B の座標を求めなさい。ただしBの $x$ 座標は正とします。

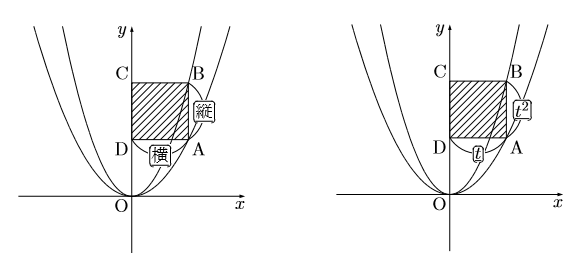
【考え方】まずは起点となる点を決める。ここではAを起点(基準)に話を進めていく。 Aの $x$ 座標を文字 $t$ とすると, Aの座標は, A( $t$ , $t^2$ )と表せる。このとき, AとBの $x$ 座標は等しいので, Bの座標を $t$ で表すとB( $t$ , $2t^2$ )となる。ここで,
$\text{AB}=2t^2-t^2=t^2$ (縦の長さ)
また, AD $=t$ (横の長さ)
(縦の長さ) $=$ (横の長さ)より,
$t^2=t$
$t^2-t=0$
$t(t-1)=0$
よって, $t=0, 1$
$t>0$ より, $t=1$
したがって, $\mathrm{B(1, 2)}$

このように正方形になる問題では, (縦の長さ) $=$ (横の長さ)とおくことで問題を解決できることが多いので, この技はぜひ習得していただきたい。入試問題でも頻出傾向にあるので, 注視しましょう。また, $x$ 軸や $y$ 軸に平行な辺の長さを求めるときは,
横方向の長さ $=$ ( $x$ 座標の大きい方)－( $x$ 座標の小さい方) $=$ (右の座標)－(左の座標)
縦方向の長さ $=$ ( $y$ 座標の大きい方)－( $y$ 座標の小さい方) $=$ (上の座標)－(下の座標)
等を用いて間違えないようにしましょう。