こんにちは。今回は宮城県の入試問題から平面図形の問題をどうぞ。
図のように, 正三角形ABCの外側に, ![]() の直角二等辺三角形ABDと
の直角二等辺三角形ABDと![]() の直角二等辺三角形CEAをつくります。次の(1)~(3)の問いに答えなさい。
の直角二等辺三角形CEAをつくります。次の(1)~(3)の問いに答えなさい。
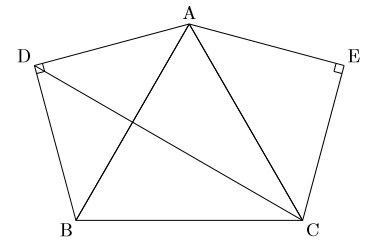
(1) ![]() の大きさを求めなさい。
の大きさを求めなさい。
(2) 点Cと点Dを結びます。![]() であることを証明しなさい。
であることを証明しなさい。
(3) 点Dと点Eを結びます。次の1, 2の問いに答えなさい。
1. ![]() の大きさを求めなさい。
の大きさを求めなさい。
2. BC![]() 4cmとするとき, 線分DEの長さを求めなさい。
4cmとするとき, 線分DEの長さを求めなさい。
(宮城)
こんにちは。今回は宮城県の入試問題から平面図形の問題をどうぞ。
図のように, 正三角形ABCの外側に, ![]() の直角二等辺三角形ABDと
の直角二等辺三角形ABDと![]() の直角二等辺三角形CEAをつくります。次の(1)~(3)の問いに答えなさい。
の直角二等辺三角形CEAをつくります。次の(1)~(3)の問いに答えなさい。

(1) ![]() の大きさを求めなさい。
の大きさを求めなさい。
(2) 点Cと点Dを結びます。![]() であることを証明しなさい。
であることを証明しなさい。
(3) 点Dと点Eを結びます。次の1, 2の問いに答えなさい。
1. ![]() の大きさを求めなさい。
の大きさを求めなさい。
2. BC![]() 4cmとするとき, 線分DEの長さを求めなさい。
4cmとするとき, 線分DEの長さを求めなさい。
(宮城)