中学数学：連立方程式の文章問題・栃木県(図形)

こんにちは。今回は栃木県の入試問題からです。それではどうぞ。

図のような。縦cm, 横cmの長方形の紙がある。この長方形に
対して次のような【操作】を行う。ただし, , は正の整数であり, とする。
【操作】
長方形の紙から短い方の辺を1辺とする正方形を切り取る。
残った四角形が正方形でない場合には, その四角形から, さらに同様の方法で正方形を切り取り,
残った四角形が正方形になるまで繰り返す。
【操作内容はここまで】
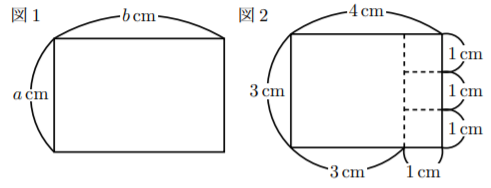
例えば, 図2のように, , の長方形の紙に対して【操作】を行うと, 1辺3\,cmの正方形の紙が1枚, 1辺1\,㎝の正方形の紙が3枚, 全部で4枚の正方形ができる。このとき, 次の問いに答えなさい。

問1 , の長方形に対して【操作】を行ったとき, できた正方形のうち最も小さい正方形の1辺の長さを求めなさい。
問2 を正の整数とする。, の長方形の紙に対して【操作】を行ったとき, 正方形は全部で何枚できるか。を用いて表しなさい。
問3 ある長方形の紙に対して【操作】を行ったところ, 3種類の大きさの異なる正方形が全部で4枚できた。これらの正方形は, 1辺の長さが長い順に, 12cmの正方形が1枚, cmの正方形が1枚, cmの正方形が2枚であった。
このとき, , の連立方程式をつくり, , の値を求めなさい。ただし, 途中の計算も書くこと。
問4 の長方形の紙に対して【操作】を行ったところ, 3種類の大きさの異なる正方形が全部で5枚できた。このとき, 考えられるの値をすべて求めなさい。
(栃木県)

プリントアウト用pdf

解答pdf