中学数学：攻略法：規則性③　かたまり

こんにちは。今回はカレンダーのような周期のある規則性についてです。

規則性：カタマリで考える

規則性の攻略(カタマリで考える。)
〇 数字が1つの周期(カタマリ)で回っていないか見る。簡単にいえば1つの数字の倍数が出てくる箇所がないか見る。
〇 他の数字はその周期(カタマリ)の数字で割った時の余りで区別できないかみる。
〇図は円形のテーブルの上に1～200までの整数を1つずつ書いたカードが置いてあり, Aから順に時計回りにAに1, Bに2, Cに3と200まで１枚ずつ配っていく。このとき次の問いに答えなさい。

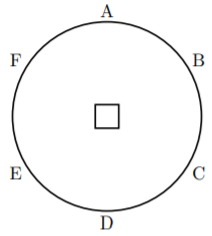
このような問題ではカタマリが威力を発揮する。この場合A, B, C, D, E, Fさんのそれぞれ取るカードを小さい順に5つ書くと
次のようになる。
Aさん1, 7, 13, 19, 25,
Bさん2, 8, 14, 20, 26,
Cさん3, 9, 15, 21, 27,
Dさん4, 10, 16, 22, 28,
Eさん5, 11, 17, 23, 29,
Fさん6, 12, 18, 24, 30,
ここでカタマリというのはFさんのカード(6の倍数)を見てもわかるように6で1周期(1カタマリ)として考える。
言い換えると, 6で割ったときの余りに注目して解くとスッキリすることが多い。
例えば200のカードは誰が取りますか。という問いに対して、200を6で割ったときの余りを考える。
2006332で、余り2である。余り2のカードを取るのは常にBさんであるから200のカードもBさんが取ることになり回答を得る。
また、Dさんが回目に取るカードをを使って表すという問いに対しては, 規則性の攻略(差が一定・等差数列)を見てもらったらわかるように,
左(小さい数字)と右(大きい数字)の差が常に一定で6であるから, として, 最初の数字が4なので6にを足せば4になることから,
となる。

規則性はまだまだある

規則性はこれで終りではない。様々なパターンの問題があるので, いろんなパターンを解いておく必要がある。
特に過去問で頻出傾向にあるところは抑えておきたい問題である。
余談ではあるが, 最も身近なカタマリはカレンダーです。カレンダーには必ず7の段(7の倍数)の曜日があります。
他の曜日は7で割ったときの余りで区別できます。カレンダー…気になったら見てくださいね。