こんにちは。複素数平面上でマイナスかけるマイナスがプラスになることを説明してみました。備忘録です。間違ってたら教えてください。
90°回転を2回行う
複素数平面上で![]() を正の方向に90
を正の方向に90![]() 回転させることを考えると
回転させることを考えると![]()
これをさらに正の方向に90![]() 回転させると
回転させると![]()
①, ②の作業によって![]() は正の方向に180
は正の方向に180![]() 回転したことになるので,
回転したことになるので,
①, ②の作業を1度でする式は次の式になります。![]()
この答えは②と一致するので, ![]()
複素数平面上の![]() を文字
を文字![]() で置き換えると, 結果
で置き換えると, 結果![]()
一般化してみると
![]() の場合の説明は,
の場合の説明は,
複素数平面上の![]() を
を![]() 拡大しながら正の方向に90
拡大しながら正の方向に90![]() の回転を2回行えばよいので,
の回転を2回行えばよいので, 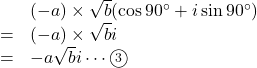
さらに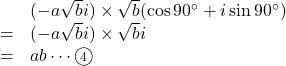
よって, ③, ④は![]() に
に![]() をかけることと同じなので,
をかけることと同じなので, ![]()
こんな感じですかね。
おかしかったら教えてください。
お粗末でした。
 数樂管理人のブログ
数樂管理人のブログ 

