こんにちは。今回は![]() 角形
角形![]() の対角線の本数が何で
の対角線の本数が何で![]() (本)で求められるか書いていこうと思います。中学数学としていますが, 高校数学で習うかもしれません。
(本)で求められるか書いていこうと思います。中学数学としていますが, 高校数学で習うかもしれません。
まず, 五角形の対角線の本数を見ることで, ![]() 角形へと一般化していこうと思います。
角形へと一般化していこうと思います。
以下の図のように5角形の1つの頂点Aからは2本の対角線AC, ADが引けます。
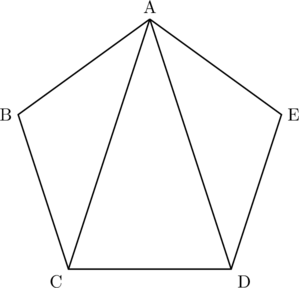
これはどういうことかと言いますと, 1つの頂点から引ける対角線は, 自分自身(今回なら頂点A)とその両隣(頂点B, E)の3つには対角線は引けないことになります。したがって, 5角形の5つの頂点から3つを引いた2つの頂点に対角線が引けるので![]() (本)の対角線が引けます。
(本)の対角線が引けます。
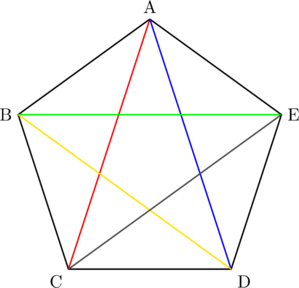
そこで単純に, 5角形の場合, 2本の対角線が引ける頂点が5つあるので, 対角線の総本数を![]() (本)としてしまうと誤りになります。それはなぜかと言うと, 対角線ACというものは, 頂点Aからも, 頂点Cからも引くことができるので, 先の計算では, 同じ対角線を2回数えてしまいます(2本重なってしまいます)。この現象はすべての対角線に言えることなので, 10を2で割ります。したがって5角形の対角線の総本数は
(本)としてしまうと誤りになります。それはなぜかと言うと, 対角線ACというものは, 頂点Aからも, 頂点Cからも引くことができるので, 先の計算では, 同じ対角線を2回数えてしまいます(2本重なってしまいます)。この現象はすべての対角線に言えることなので, 10を2で割ります。したがって5角形の対角線の総本数は![]() (本)となります。
(本)となります。
一般化すると,
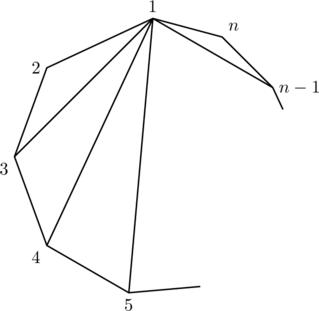
よって
となります。
n角形の対角線の総本数
![]() (本)
(本)
 数樂管理人のブログ
数樂管理人のブログ 

