こんにちは。三平方の定理(ピタゴラスの定理)が成り立つことを相似を用いて証明しよう。
三平方の定理(ピタゴラスの定理)は以下のような定理です。
三平方の定理(ピタゴラスの定理)
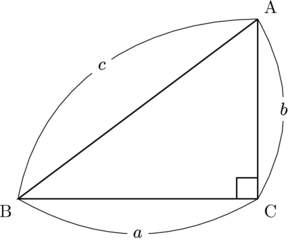
直角三角形の斜辺を![]() , 直角を挟む2辺を
, 直角を挟む2辺を![]() ,
, ![]() とすると,
とすると,
![]()
が成り立ちます。この関係を三平方の定理(ピタゴラスの定理)といいます。
相似を用いてこれを証明していきましょう。
以下のように直角三角形ABCの頂点Cから辺ABに垂線を下ろし, 交点をDとします。AB![]() , BC
, BC![]() , CA
, CA![]() , BD
, BD![]() とします。
とします。
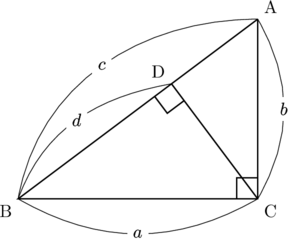
このとき, △ABC∽△CBD(2組の角がそれぞれ等しい)から, 次の辺の比が言えます。
AB : CB
これより
また, △ABC∽△ACD(2組の角がそれぞれ等しい)から, 次の辺の比が言えます。
AB : AC
AD
これより
が得られる。(終わり)
面積の関係を用いて証明していきましょう。
以下のように斜辺が![]() , 直角を挟む2辺が
, 直角を挟む2辺が![]() ,
, ![]() の合同な直角三角形を4枚用意して, 図のように並べて, 1辺が
の合同な直角三角形を4枚用意して, 図のように並べて, 1辺が![]() の正方形ABCDをつくりました。
の正方形ABCDをつくりました。
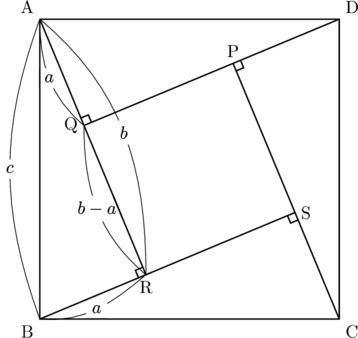
このとき, 外側の正方形の1辺であるABはAB
この正方形ABCDの面積
1辺
また, この正方形ABCDの面積
が成り立つ。(終わり)
以下のように直角三角形ABCの頂点Cから辺ABに垂線を下ろし, 交点をDとします。AB![]() , BC
, BC![]() , CA
, CA![]() とします。
とします。
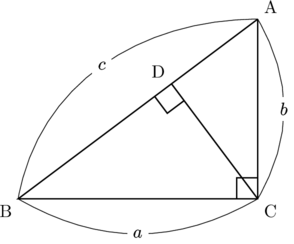
このとき, △CDB∽△ADC∽△ACB(2組の角がそれぞれ等しい)であるから, 次の相似比がいえます。
△CDB:△ADC:△ACBの相似比は
ここで, 面積比は相似比の2乗であるから,
△CDB(
がいえ, 面積の関係より,
が成り立つ。(終わり)
 数樂管理人のブログ
数樂管理人のブログ 

