こんにちは。相城です。高校生になってつまづきやすい1つが, この2次関数の場合分けです。今回は定義域が固定で, 軸が移動してくる場合を書いてみたいと思います。グラフ画像はイメージです。
以下, 例題を見ながら場合分けの方法を書いていきますね。
例題:2次関数![]() の最小値を求めなさい。
の最小値を求めなさい。
まず, 式を平方完成すると,![]()
となるので, 2次関数の軸は![]() ということが分かります。軸が文字(変数)になるので, この軸がどこにあるかで, 最小値をとる
ということが分かります。軸が文字(変数)になるので, この軸がどこにあるかで, 最小値をとる![]() の値が変わってきます。結論から言うと, この場合, 2次関数の軸が定義域の左側, 内側, 右側の3パターンで分けて考えます。
の値が変わってきます。結論から言うと, この場合, 2次関数の軸が定義域の左側, 内側, 右側の3パターンで分けて考えます。
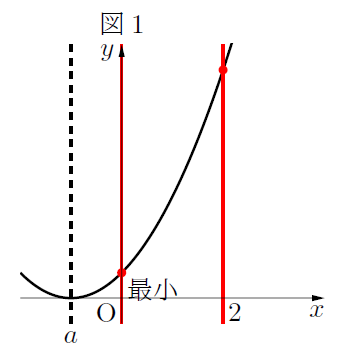
場合分け①:![]() (軸が定義域の左側にあるとき)
(軸が定義域の左側にあるとき)
最小値は![]() のときなので,
のときなので, ![]() に
に![]() を代入すると, 最小値は
を代入すると, 最小値は![]() となります。
となります。
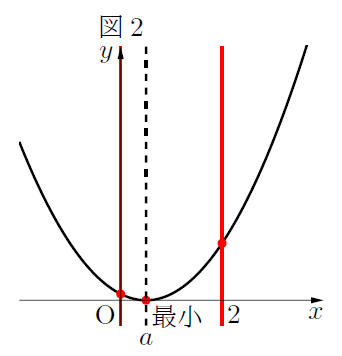
場合分け②:![]() (軸が定義域の内側(両端含む)にあるとき)
(軸が定義域の内側(両端含む)にあるとき)
最小値は![]() のときなので, この場合は平方完成した式に代入するのが手っ取り早いので,
のときなので, この場合は平方完成した式に代入するのが手っ取り早いので, ![]() に
に![]() を代入すると, 最小値は
を代入すると, 最小値は![]() になります。
になります。
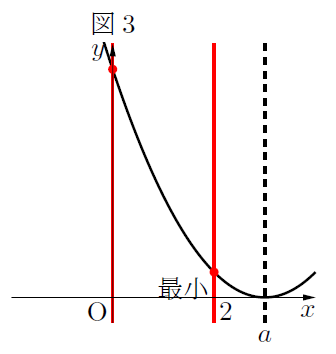
場合分け③:![]() (軸が定義域の右側にあるとき)
(軸が定義域の右側にあるとき)
最小値は![]() のときなので,
のときなので, ![]() に
に![]() を代入すると, 最小値は
を代入すると, 最小値は![]() となります。
となります。
場合分けと最小値をとる![]() の値を表にすると以下のようになります。
の値を表にすると以下のようになります。
例題:2次関数![]() の最大値を求めなさい。
の最大値を求めなさい。
まず, 式を平方完成すると,![]()
となり, 最小値と同じように, 軸![]() の場合分けを行っていきます。
の場合分けを行っていきます。
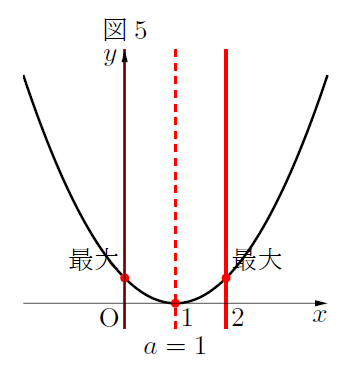
ただ, 場合分けの方法は, 最小値と全く同じというわけではありません。よく図を見ていると, 最大値をとる![]() の値は, 軸
の値は, 軸![]() が定義域のちょうど真ん中の
が定義域のちょうど真ん中の![]() より小さいときまでは,
より小さいときまでは, ![]() で最大値をとり, 次に軸
で最大値をとり, 次に軸![]() が
が![]() と一致するとき
と一致するとき![]() で最大値が一致し, 軸
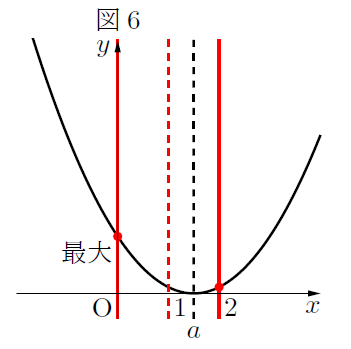
で最大値が一致し, 軸![]() が
が![]() より大きいとき
より大きいとき![]() で最大値をとるようになるので, その3パターンで場合分けします。
で最大値をとるようになるので, その3パターンで場合分けします。
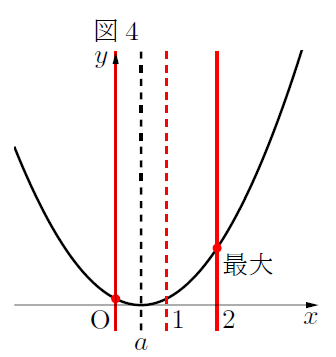
場合分け①:![]() (軸が定義域の真ん中より左側にあるとき)
(軸が定義域の真ん中より左側にあるとき)
最大値は![]() のときなので,
のときなので, ![]() に
に![]() を代入すると, 最大値は
を代入すると, 最大値は![]() となります。
となります。
場合分け②:![]() (軸が定義域の真ん中と一致するとき)
(軸が定義域の真ん中と一致するとき)
![]() の
の![]() なので,
なので, ![]() になります。
になります。![]() で同じ値をとるので, 求めやすい方を代入(
で同じ値をとるので, 求めやすい方を代入(![]() を代入)して, 最大値は
を代入)して, 最大値は![]() となります。
となります。
場合分け③:![]() (軸が定義域の真ん中より右側にあるとき)
(軸が定義域の真ん中より右側にあるとき)
最大値は![]() のときなので,
のときなので, ![]() に
に![]() を代入すると, 最大値は
を代入すると, 最大値は![]() となります。
となります。
場合分けと最大値をとる![]() の値を表にすると以下のようになります。
の値を表にすると以下のようになります。
例題:2次関数![]() の最大値を求めなさい。
の最大値を求めなさい。
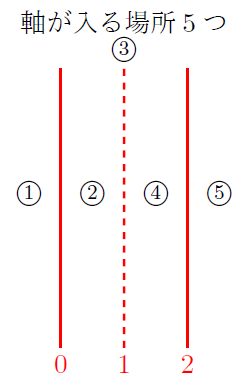
この問題で難しいのは, このように最小値と最大値をまとめて問われる場合で, この場合, 最大5パターンに分けます。分け方は, これまで書いてきた最小値と最大値を組み合わせた場合なので, それぞれで場合分けを行った, ![]() それ以外で範囲を分けます。すると, 以下の5パターンに分類されます。
それ以外で範囲を分けます。すると, 以下の5パターンに分類されます。
軸が入る場所を順に図で表すと以下のようになります。
これが最大5パターンになる分け方です。以下に5パターンを簡単に記しておきます。グラフはイメージを掴むためのもので正確でありません。
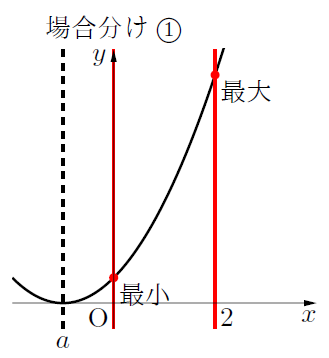
場合分け①:![]() のとき
のとき
最小値:![]() のとき,
のとき, ![]()
最大値:![]() のとき,
のとき, ![]()
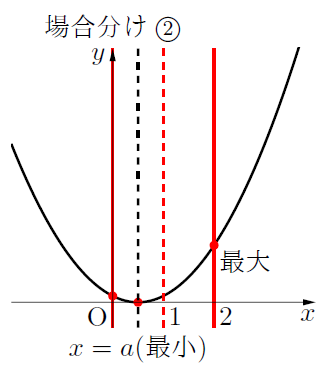
場合分け②:![]() のとき
のとき
最小値:![]() のとき,
のとき, ![]()
最大値:![]() のとき,
のとき, ![]()
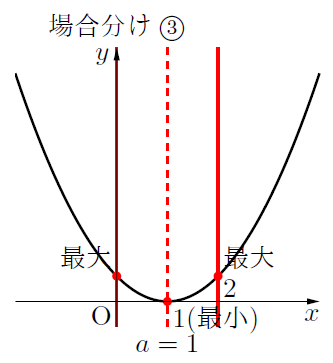
場合分け③:![]() のとき (軸と定義域の中心が一致するとき)
のとき (軸と定義域の中心が一致するとき)![]()
最小値:![]() のとき,
のとき, ![]()
最大値:![]() のとき,
のとき, ![]()
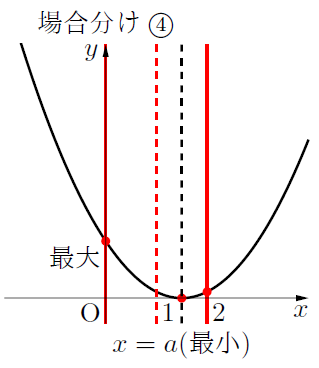
場合分け④:![]() のとき
のとき
最小値:![]() のとき,
のとき, ![]()
最大値:![]() のとき,
のとき, ![]()
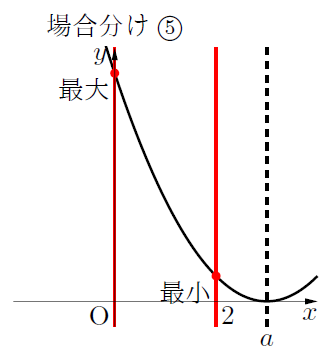
場合分け⑤:![]() のとき
のとき
最小値:![]() のとき,
のとき, ![]()
最大値:![]() のとき,
のとき, ![]()
以上になります。
以下は定義域が動く場合の場合分けの記事です。
 高校数学:2次関数の場合分け・定義域が動く
高校数学:2次関数の場合分け・定義域が動く 数樂管理人のブログ
数樂管理人のブログ