高校数学：十分条件,必要条件,必要十分条件

こんにちは。相城です。十分条件, 必要条件と必要十分条件についてかみくだいて書いておきます。例題を見ながら書いていきます。家庭学習のご参考にしてくれれば幸いです。

pはqであるための

基本的な見方は以下のようになります。

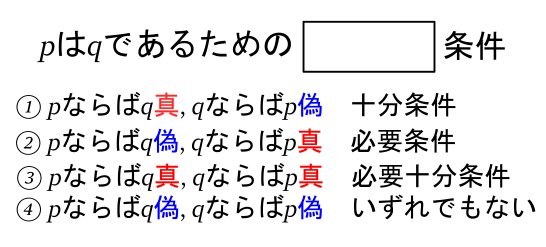
①十分条件

命題を普通に読んで成り立つが, 逆にすると成り立たない場合
例題 $x=0$ は $xy=0$ であるための(　　　)条件
【見方】
命題： $x=0$ ならば $xy=0$ は真
逆： $xy=0$ ならば $x=0$ は偽(反例 $y=0$ )
したがって, 逆は成り立たないので十分条件になります。

②必要条件

命題を普通に読んで成り立たないが, 逆にすると成り立つ場合
例題 $a+b$ が偶数であることは, $a$ , $b$ が偶数であるための(　　　)条件
【見方】
命題： $a+b$ が偶数ならば $a$ , $b$ は偶数は偽(反例 $a$ も $b$ も奇数),
逆： $a$ , $b$ が偶数ならば $a+b$ は偶数は真
したがって, 逆の場合のみ成り立つので必要条件になります。

③必要十分条件

命題を普通に読んでも, 逆にして読んでも成り立つ場合
例題： $x^2-6x+9=0$ は, $x=3$ であるための(　　　)条件
【見方】
命題： $x^2-6x+9=0$ ならば, $x=3$ は真
方程式の解は $(x-3)^2=0$ で $x=3$ しか存在しないので。
逆： $x=3$ ならば $x^2-6x+9=0$ は真
$x=3$ を $x^2-6x+9$ に代入すると0になるので。
したがって, この場合, 必要十分条件になります。

④いずれでもない

上記①, ②, ③のどれにも当てはまらない場合, この解答になります。
例題： $x=3$ は $x$ が偶数であるための(　　　)条件
【見方】
命題： $x=3$ ならば $x$ が偶数は偽(反例 $x$ は奇数)
逆： $x$ が偶数ならば $x=3$ は偽(反例 $x=2$ )
したがって, この場合, いずれでもないとなります。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル