高校数学：集合と命題の入り口

こんにちは。相城です。今回は集合と命題について少し書いておきます。

命題とは

命題とは, ある事柄が正しいか正しくないか定まる文のこと指します。
命題が正しいことを, 命題は真であるといい, 正しくないことを命題は偽であるといいます。

例題

例題①, ②を見ていきましょう。
次の命題の真偽を言いなさい。
①四角形の内角の和は180 $^{\circ}$ である。
この命題は偽である。
②正三角形の1つの内角は60 $^{\circ}$ である。
この命題は真である。

命題p⇒q

命題 $p\Longrightarrow q$
$p$ ならば $q$ の形を $p\Longrightarrow q$ と表します。
このとき, $p$ は仮定, $q$ は結論と言います。

命題 $p\Longrightarrow q$ が真
この場合, 条件 $p$ を満たす集合 $P$ が, 条件 $q$ を満たす集合 $Q$ にすべて含まれることを意味します。

命題 $p\Longrightarrow q$ が偽
この場合, 条件 $p$ を満たす集合 $P$ の一部または全部が, 条件 $q$ を満たす集合 $Q$ に含まれていないことを意味します。Qに含まれていないものの例を1つ示すことで偽であることが保証されます。その例を反例といいます。

例題

例題①, ②を見ていきまでょう。
①実数 $x$ に関する条件で, $p : x\geqq 4,\hspace{3mm}q : x\geqq 0$
こういう問題では数直線上に表してみるとわかります。

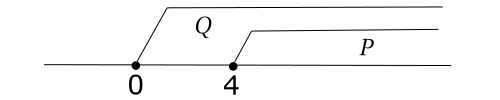
したがってこの場合, 上の数直線から $P\subset Q$ なので, この命題は真になります。

②自然数 $n$ に関して, $p$ : $n$ が4の倍数 $\hspace{3mm},\ 　q$ : $n$ が8の倍数
この場合, 条件 $p$ を満たす集合 $P$ の要素は
$P=\{4, 8, 12, 16, \cdots\}$
条件 $q$ を満たす集合 $Q$ の要素は
$Q=\{8, 16, 24, 32, \cdots\}$
このとき, $4\in P$ (4は $P$ に属している)ですが, $4\notin Q$ (4は $Q$ に属さない)なので, $Q$ に $P$ すべての要素が含まれません。したがって, この命題は偽になります。反例は $4\in P$ , $4\notin Q$

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル