こんにちは。相城です。今回は三角比について書いておきます。
![]() ,
, ![]() ,
, ![]() も円で考えれば, 間違いが減るのではないでしょうか。もちろん, 基本的な考え方は, 45
も円で考えれば, 間違いが減るのではないでしょうか。もちろん, 基本的な考え方は, 45![]() , 45
, 45![]() , 90
, 90![]() や30
や30![]() , 60
, 60![]() , 90
, 90![]() の直角三角形をイメージして考えるのですが。
の直角三角形をイメージして考えるのですが。
円を使ってsin,cos,tan
以下のような半径![]() の円があって, その円周上の点をP(
の円があって, その円周上の点をP(![]() ,
, ![]() )とする。
)とする。![]() とするとき,
とするとき, ![]() ,
, ![]() ,
, ![]() は以下の式で求められます。
は以下の式で求められます。
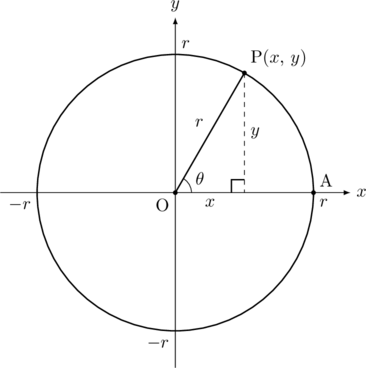
定義
![]()
ただし,
図の
円を使って求めてみよう
せっかくなので, 少し例題をやってきまでょう。
次の値を求めなさい。![]() ,
, ![]() ,
, ![]()
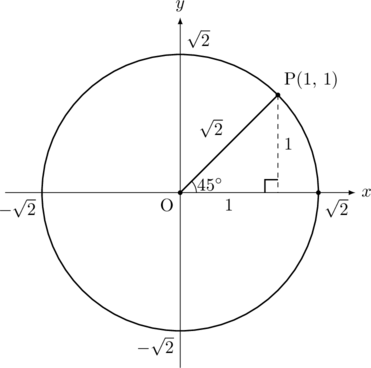
次の値を求めなさい。![]() ,
, ![]() ,
, ![]()
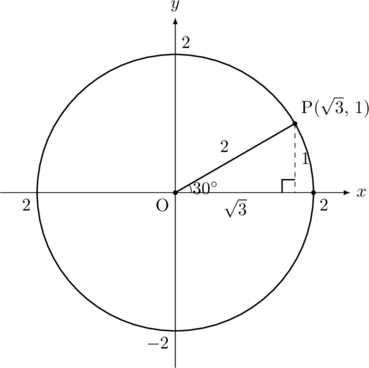
次の値を求めなさい。![]() ,
, ![]() ,
, ![]()
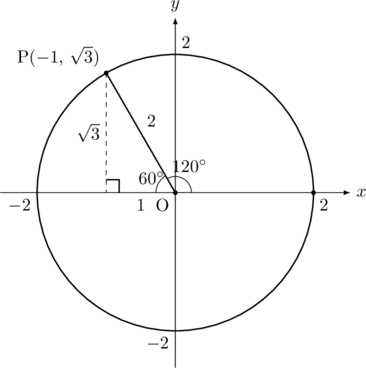
 数樂管理人のブログ
数樂管理人のブログ 

