こんにちは。今回は三角比の相互関係を書いておきますね。
高1のときに習うものを中心に書いておきます。
三角比の相互関係
覚えておきたい三角比の関係式
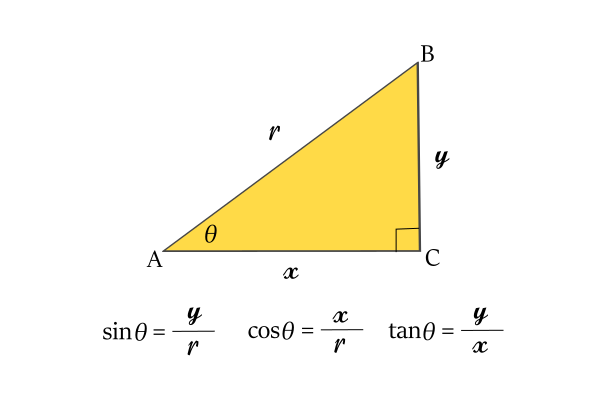
![]() に関してはこちらの記事をご参照ください。
に関してはこちらの記事をご参照ください。![]() は
は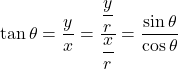
として得られます。
また, この式から![]()
という式が得られます。![]() は
は![]() の両辺を
の両辺を![]() で割れば
で割れば![]()
![]()
![]()
として公式が得られます。
また, ![]() を変形すると
を変形すると![]()
という式が得られます。
この式変形のとき, 知っておくと便利なテクニックは![]() という等式で. AとBを入れ替えても等式は成り立つというものです。つまり,
という等式で. AとBを入れ替えても等式は成り立つというものです。つまり, ![]()
これは, 知っておくと便利です。
知っておくと便利なテクニック
これの基本として,
があることを知っておきましょう。
例題をやってみよう
例題1:![]() のとき,
のとき, ![]() ,
, ![]() を求めなさい。ただし,
を求めなさい。ただし, ![]() とする。
とする。
解法:まず, ![]() に
に![]() を代入すると,
を代入すると, ![]()
![]()
![]()
![]()
![]() の場合
の場合![]()
![]() の場合
の場合![]()
![]() で答えが2つあるのは,
で答えが2つあるのは, ![]() の範囲では, 鋭角
の範囲では, 鋭角![]() と鈍角
と鈍角![]() の2つあるから。
の2つあるから。
例題2:![]() のとき,
のとき, ![]() ,
, ![]() を求めなさい。ただし,
を求めなさい。ただし, ![]() とする。
とする。
解法:まず, ![]() に
に![]() を代入すると,
を代入すると,![]()
![]()
![]()
![]()
![]()
![]() で答えが1つ(正だけ)なのは,
で答えが1つ(正だけ)なのは, ![]() の範囲では,
の範囲では, ![]() だから。
だから。
例題3:![]() のとき,
のとき, ![]() ,
, ![]() を求めなさい。ただし,
を求めなさい。ただし, ![]() とする。
とする。
解法:![]() が与えられたときは,
が与えられたときは, ![]() を
を![]() としてを使うと便利です。
としてを使うと便利です。
この式に![]() を代入すると,
を代入すると, 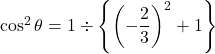
![]()
![]()
![]() より,
より, ![]() だから,
だから, ![]()
![]() より,
より, ![]()
以上になります。
 数樂管理人のブログ
数樂管理人のブログ 

