こんにちは。相城です。今回は三角比において![]() の部分が
の部分が![]() になった場合, どのような関係になるか見ていきましょう。
になった場合, どのような関係になるか見ていきましょう。
180°-θの三角比
結論から書いておきます。
180°ーθの三角比
180°-θの三角比のなぜ
斜辺![]() ,対辺(高さ)
,対辺(高さ)![]() , 隣辺(底辺)
, 隣辺(底辺)![]() とし, 斜辺と隣辺(底辺)のなす角を
とし, 斜辺と隣辺(底辺)のなす角を![]() とする。
とする。
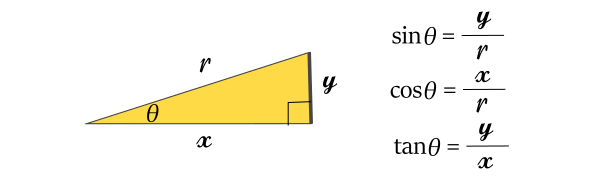
この直角三角形を![]() 平面上に隣辺(底辺)が
平面上に隣辺(底辺)が![]() 軸と接し,
軸と接し, ![]() を持つ頂点が原点と重なるようにように設置する。
を持つ頂点が原点と重なるようにように設置する。
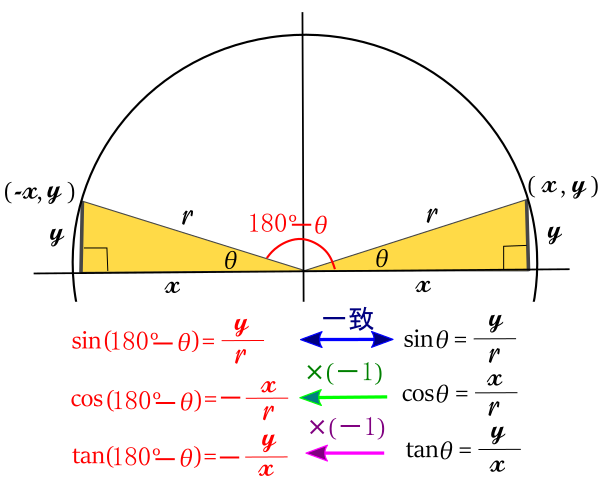
このとき, 原点を中心とし, 半径![]() の円を描くと図のようになり, 円と三角形が接してできる点の座標は(
の円を描くと図のようになり, 円と三角形が接してできる点の座標は(![]() ,
, ![]() )となります。
)となります。
また, ![]() は先の直角三角形を
は先の直角三角形を![]() 軸について対称に配置してできる図中の赤い色の角になります。このとき,
軸について対称に配置してできる図中の赤い色の角になります。このとき, ![]() 軸について対称移動した三角形と円が接してできる座標は図より(
軸について対称移動した三角形と円が接してできる座標は図より(![]() ,
, ![]() )となります。
)となります。
![]() ,
, ![]() において, それぞれ
において, それぞれ![]() ,
, ![]() ,
, ![]() を求めると,
を求めると,![]()
![]()
![]()
![]()
![]()
![]()
これから![]() と
と![]() ,
, ![]() と
と![]() が一致し,
が一致し, ![]() と
と![]() が一致します。
が一致します。
以上より![]()
![]()
![]()
が得られます。
 数樂管理人のブログ
数樂管理人のブログ 

