こんにちは。相城です。今回は3辺が分かる三角形の面積の求め方を書いておきます。
3辺が分かる三角形の面積
3辺の長さが4, 5, 6である三角形の面積を求めなさい。
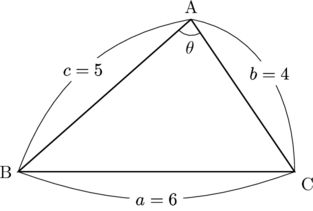
今回は
余弦定理から得られる![]() に
に![]() ,
, ![]() ,
, ![]() を代入すると,
を代入すると, ![]()
![]()
![]() を
を![]() に代入して,
に代入して, ![]()
![]()
![]()
![]() なので,
なので, ![]()
よって△ABCの面積![]() は
は![]()
![]()
流れをつかんでおこう
- 余弦定理から
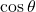 の値を求める。
の値を求める。 - 上で求めた
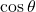 の値を
の値を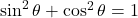 に代入して,
に代入して, 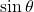 の値を求める
の値を求める - 面積の公式
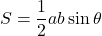 を用いて求める
を用いて求める
こんにちは。相城です。今回は3辺が分かる三角形の面積の求め方を書いておきます。
3辺が分かる三角形の面積
3辺の長さが4, 5, 6である三角形の面積を求めなさい。

余弦定理から得られる![]() に
に![]() ,
, ![]() ,
, ![]() を代入すると,
を代入すると, ![]()
![]()
![]() を
を![]() に代入して,
に代入して, ![]()
![]()
![]()
![]() なので,
なので, ![]()
よって△ABCの面積![]() は
は![]()
![]()