こんにちは。相城です。今回は三角形の内接円の半径の求め方を書いておきます。
3辺の長さが![]() ,
, ![]() ,
, ![]() で,
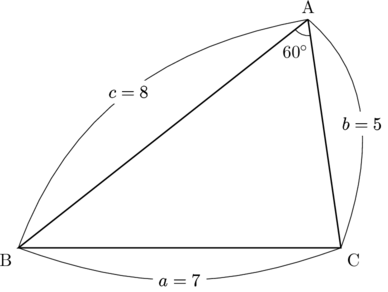
で, ![]() である三角形ABCに内接する円の半径を求めなさい。
である三角形ABCに内接する円の半径を求めなさい。
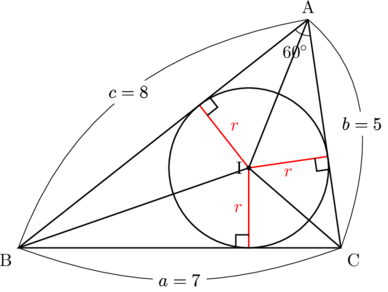
内接円の半径を![]() とすると,
とすると, ![]() は次の図のように, 各辺に垂直(接線と接点を通る円の半径のつくる角は
は次の図のように, 各辺に垂直(接線と接点を通る円の半径のつくる角は![]() )になります。
)になります。
方針
上の図の (赤の線分)を求めるのに, △ABCの面積を求めます。
(赤の線分)を求めるのに, △ABCの面積を求めます。
次に, △ABCの面積は△IAB, △IBC, △ICAの面積の和としても求められます。このとき, は△IAB, △IBC, △ICAの高さになっているので, この3つの三角形の面積を
は△IAB, △IBC, △ICAの高さになっているので, この3つの三角形の面積を を用いて表し,
を用いて表し,
△IAB △IBC
△IBC △ICA
△ICA △ABC
△ABC
として方程式をつくり, を求めます。
を求めます。
次に, △ABCの面積は△IAB, △IBC, △ICAの面積の和としても求められます。このとき,
△IAB
として方程式をつくり,
【解答例】
△ABCの面積![]() は
は![]()
ここで
△IAB![]()
△IBC![]()
△ICA![]()
![]() △IAB
△IAB![]() △IBC
△IBC![]() △ICA
△ICA![]()
![]() なので,
なので, ![]()
![]()
よって, 内接円の半径は![]()
このとき, 今回は分かりやすいように, 3つの三角形(△IAB, △IBC, △ICA)を分けて求めましたが, 理解が深まると, 3つの三角形(△IAB, △IBC, △ICA)の和は次の式で得られます。![]() ・・・(覚えておくと便利)
・・・(覚えておくと便利)
今回の問題であれば![]()
計算が少し楽ですね。
流れをつかんでおこう
- 円に外接する三角形の面積を求める。
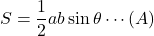
- 内接する円の半径を
 (文字)として, 内心と三角形の頂点を結んでできる3つの三角形の和を
(文字)として, 内心と三角形の頂点を結んでできる3つの三角形の和を (文字)で表す。
(文字)で表す。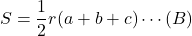
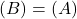 , つまり,
, つまり,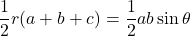 として
として を求める。
を求める。
3辺に未知数の辺があるとき
円に外接する三角形に長さがまだわかっていない辺を含むときは, 余弦定理などで求めてから, この解法に持ち込むといいでしょう。
 数樂管理人のブログ
数樂管理人のブログ 

