こんにちは。相城です。今回は簡単なテクニックをご紹介します。角出しというテクニックです。実際に例題を見ながらやっていきましょう。また, 最後に角出しを使った問題をおいておきますので, 実際に解いてみてください。
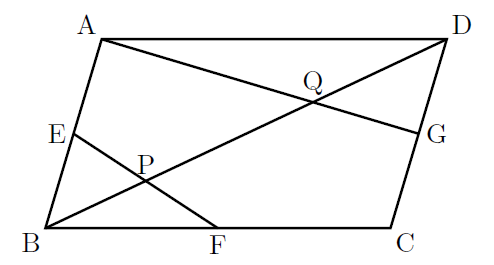
下の平行四辺形ABCDで, 辺AB, BC, CDの中点をそれぞれ, E, F, Gとし, 対角線BDとEF, AGとの交点をそれぞれP, Qとする。BD![]() 12cmのとき, BPの長さを求めなさい。
12cmのとき, BPの長さを求めなさい。
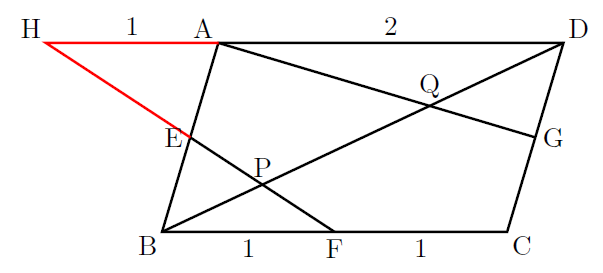
この場合, BPを含んだ相似形の三角形がありません。このように求めたい線分を含む相似形がないときは, 以下の赤線部のように角出し(図形の外部にはみだし)をして, BPを含む三角形の相似形(△BFP∽△DHP)をつくります。これが角出しのテクニックになります。こうすることで, BPがいつもの相似形に落ち着き, BPが平易に求められるようになります。
この図では, BF : FC![]() 1 : 1, なので, AD
1 : 1, なので, AD![]() 2と考えることができます。
2と考えることができます。
EがABの中点なので, △BFE![]() △AHE(1組の辺とその両端の角)より,
△AHE(1組の辺とその両端の角)より,
BF : AH![]() 1 : 1となる。△BFP∽△DHPであり, その相似比はBF : DH
1 : 1となる。△BFP∽△DHPであり, その相似比はBF : DH![]() 1 : 3なので, BP : DP
1 : 3なので, BP : DP![]() 1 : 3となる。よって,
1 : 3となる。よって,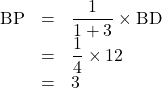
BP![]() 3cm
3cm
となります。
※もちろんEFとDCの延長線が交わるように角出ししても大丈夫です。
角出しテクニック
求めたい線分を含む相似形を図形外部につくり出すこと。その際に図形の外側に角が出るようになるのでその名前が付いたと思われる。
 中学数学:相似:比・面積比・体積比の問題④
中学数学:相似:比・面積比・体積比の問題④  中学数学:相似:比・面積比・体積比の問題⑤
中学数学:相似:比・面積比・体積比の問題⑤  中学数学:相似:比・面積比・体積比の問題⑨
中学数学:相似:比・面積比・体積比の問題⑨ 数樂管理人のブログ
数樂管理人のブログ 


BP= の所でなんで×12をするのですか?
問題文が間違っていました。BP=12ではなく、BD=12でした。
ご指摘ありがとうございます。