高校数学：同じものを含む順列

こんにちは。相城です。今回は同じものを含む順列について書いておきますね。

同じものを含む順列について

同じ文字を含む順列とは

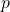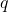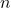同じものが $p$ 個, $q$ 個, $r$ 個で合計 $n$ 個あるとき, それ全部を1列に並べる順列の総数は,
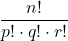$\dfrac{n!}{p!\cdot q!\cdot r!}$ 　ただし, $p+q+r=n$
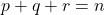
で計算できます。

例題を見てみよう

【例題】AAABBCの6個の文字を1列に並べる場合, 何通りの並べ方があるか。
この場合, AAAは区別できないため, 並び方はAAAの1通りしかありません。ただ通常の順列 $n!$ では, AAAをA $_1$ , A $_2$ , A $_3$ と区別するためA $_1$ A $_2$ A $_3$ の3つを1列に並べる並べ方の総数 $3!$ のダブりが生じてしまいます。Bも同様に2つあるので, $2!$ 通りのダブりが生じます。最後のCは1個なのでダブりは生じません。このように, 上の公式では一旦区別できるものとして, 1列に並べ, その後, ダブりの個数で割って総数を求めていることになります。
したがって, 例題の解答は,
$\dfrac{6!}{3!\cdot2!\cdot1!}=60$
60通りとなります。

並べるけど組合せを使う

上の問題って, 6つの文字を置く場所〇〇〇〇〇〇があって, その中からAを置く場所を3か所選んで, Aを置き, 残った3か所からBを置く場所を2か所選んで, Bを置き, 残ったところにCを置けばいいことになります。置くものは区別でいないので, 置き方は常に1通りに決まります。下図参照。

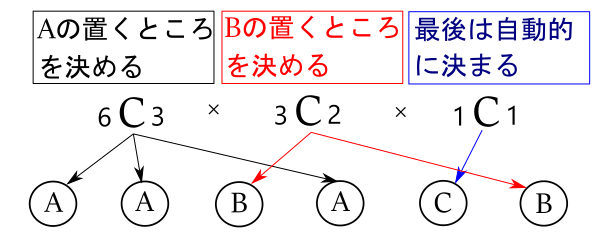
式で表すと
${}_{6} \mathrm{C}_3\times{}_{3} \mathrm{C}_2\times {}_{1} \mathrm{C}_1=\underline{\dfrac{6\cdot5\cdot4}{3\cdot2\cdot1}\times\dfrac{3\cdot2}{2\cdot1}\times\dfrac{1}{1}}=60$
60通り
※下線部はまさに $\dfrac{6!}{3!\cdot2!\cdot1!}$ になっていますね。
それでは。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル