高校数学：最短経路の場合の数

こんにちは。相城です。今回は最短経路の場合の数についてです。
同じものを含む順列と同じ考え方ですので, 理屈などはそちらの記事をご参照ください。

例題を見てみよう

以下の図で, 地点Aから地点Bまで最短で行く経路は, 全部で何通りあるか求めよ。

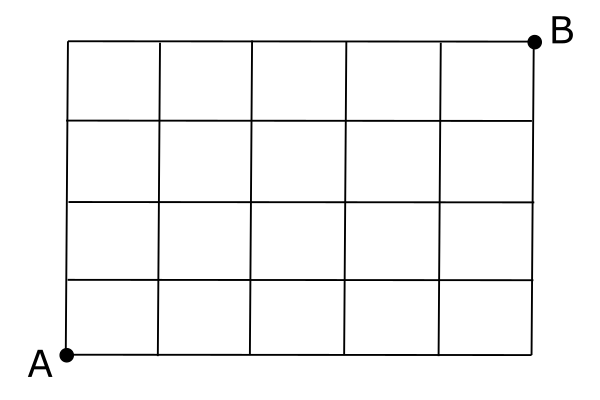
【解法】この場合, 上に行く矢印↑が4つと, 右に行く矢印→が5つあれば, 目的の地点Bにつくので, ↑↑↑↑→→→→→の順列を考えるとよい。

$\dfrac{9!}{4!\cdot5!}=126$
もしくは, 9個のうち4つ選んで↑を並べればいいので,
${}_9 \mathrm{C}_4=126$
126通りとなります。

例題を見てみよう

以下の図で, 地点Aから地点Cを通って地点Bまで最短で行く経路は, 全部で何通りあるか求めよ。

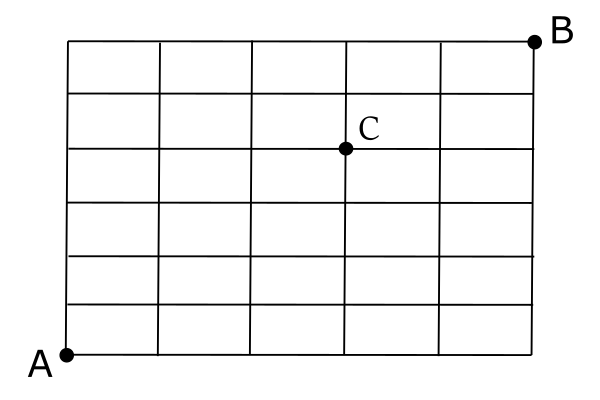
【解法】この場合, 地点Aから地点Cまで行く最短経路の総数と地点Cから地点Bまで行く最短経路の総数を積の法則にしたがって計算すればよい。

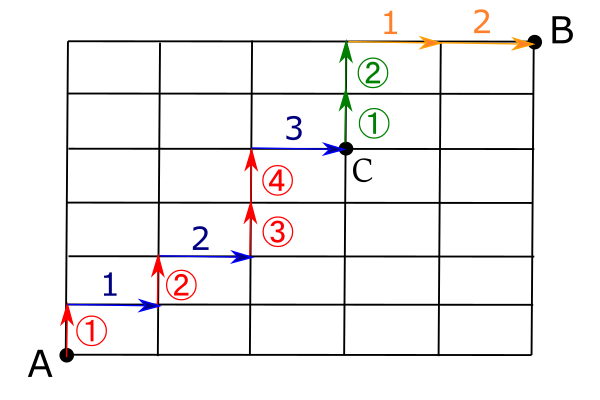
したがって, 地点Aから地点Cまででは, 上に行く矢印↑が4つと, 右に行く矢印→が3つあれば, 目的の地点Cにつくので, ↑↑↑↑↑→→→の順列を考えるとよい。 $\dfrac{7!}{4!\cdot3!}$ 通り。
また, 地点Cから地点Bまでは, 上に行く矢印↑が2つと, 右に行く矢印→が2つあれば, 目的の地点Bにつくので, ↑↑→→の順列を考えるとよい。 $\dfrac{4!}{2!\cdot2!}$ 通り。
これら2つの事柄は同時に起こるので, 積の法則にしたがって, 求める最短経路の総数は,
$\dfrac{7!}{4!\cdot3!}\times\dfrac{4!}{2!\cdot2!}=35\times6=210$
210通り

こんな感じです。

高校数学：同じものを含む順列

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル