こんにちは。今回は三角関数を含む方程式について書いておきます。例題を解きながら見ていきます。
方程式の考え方
【例①】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】![]() なので,
なので, ![]() の符号は
の符号は![]() 座標の符号で決まる。この問題では,
座標の符号で決まる。この問題では, ![]() が1でない正の数なので,
が1でない正の数なので, ![]() 座標が正の範囲である第1象限と第2象限に答がありそうなことが分かる。この解法として, 単位円を描いて考えるのが一般的?であるが, 私はあの単位円にしたとき, 座標が分数になるのが嫌いなので, 半径2の円を描いて考える。なぜ半径2の円か?それは解いていくと気づくと思うのだが,
座標が正の範囲である第1象限と第2象限に答がありそうなことが分かる。この解法として, 単位円を描いて考えるのが一般的?であるが, 私はあの単位円にしたとき, 座標が分数になるのが嫌いなので, 半径2の円を描いて考える。なぜ半径2の円か?それは解いていくと気づくと思うのだが, ![]() が出てくるのは,
が出てくるのは, ![]() の直角三角形で, 斜辺がちょうど2になっているから。そこで,
の直角三角形で, 斜辺がちょうど2になっているから。そこで, ![]() となる点を見つけて, そこから真横(
となる点を見つけて, そこから真横(![]() 軸に平行)に延ばした直線と円との交点が, 同じ
軸に平行)に延ばした直線と円との交点が, 同じ![]() (
(![]() 座標が同じだから)になる点というわけです。このように,
座標が同じだから)になる点というわけです。このように, ![]() が
が![]() となる点(
となる点(![]() 座標が
座標が![]() の点)は
の点)は![]() の範囲内に2つ(下図の赤い印)ある。
の範囲内に2つ(下図の赤い印)ある。
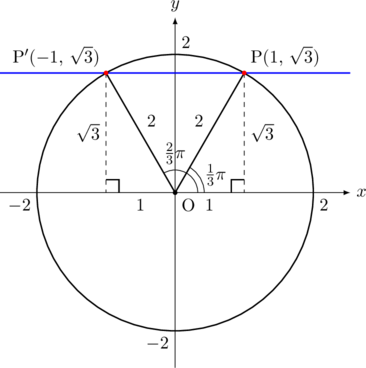
問題の答えは, 図からわかるように,
【例②】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】![]() なので, その符号は
なので, その符号は![]() 座標の符号で決まる。この問題では,
座標の符号で決まる。この問題では, ![]() の値が
の値が![]() でない負の数なので,
でない負の数なので, ![]() 座標が負の範囲である第2象限と第3象限に答がありそうなことが分かる。
座標が負の範囲である第2象限と第3象限に答がありそうなことが分かる。![]() も
も![]() を考えたときと同様に円を描いて考えるが,
を考えたときと同様に円を描いて考えるが, ![]() の分子分母に
の分子分母に![]() をかけると
をかけると![]() となるので,書く円の半径は
となるので,書く円の半径は![]() である。こうすることで,
である。こうすることで, ![]() の直角二等辺三角形に帰着できる。そこで,
の直角二等辺三角形に帰着できる。そこで, ![]() となる点を1つ見つけて, そこから真縦(
となる点を1つ見つけて, そこから真縦(![]() 軸に平行)に延ばした直線と円との交点が, 同じ
軸に平行)に延ばした直線と円との交点が, 同じ![]() (
(![]() 座標が同じだから)になる点というわけです。このように,
座標が同じだから)になる点というわけです。このように, ![]() が
が![]() となる点(
となる点(![]() 座標が
座標が![]() の点)は
の点)は![]() の範囲内に2つ(下図の赤い印)ある。
の範囲内に2つ(下図の赤い印)ある。
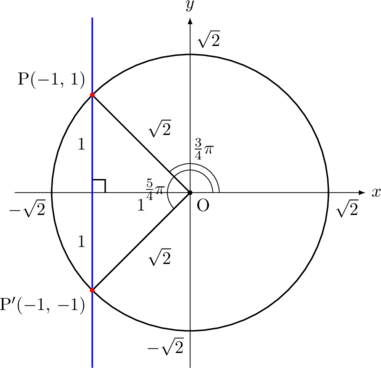
問題の答えは, 図からわかるように,
【例③】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】![]() で与えられ,
で与えられ, ![]() の値が正の数なので,
の値が正の数なので, ![]() 座標と
座標と![]() 座標の符号が一致する第1象限と第3象限に答がありそうなことが分かる。
座標の符号が一致する第1象限と第3象限に答がありそうなことが分かる。![]() も同様に円を描いて考える。そこで,
も同様に円を描いて考える。そこで, ![]() となる点を1つ見つけて, そこから原点(原点対称)の方に延ばした直線と円との交点が, 同じ
となる点を1つ見つけて, そこから原点(原点対称)の方に延ばした直線と円との交点が, 同じ![]() (
(![]() が同じ値だから)になる点というわけです。このように,
が同じ値だから)になる点というわけです。このように, ![]() が
が![]() となる点は
となる点は![]() の範囲内に2つ(下図の赤い印)ある。ちなみに, 描く円の半径は2(
の範囲内に2つ(下図の赤い印)ある。ちなみに, 描く円の半径は2(![]() の直角三角形より)である。
の直角三角形より)である。
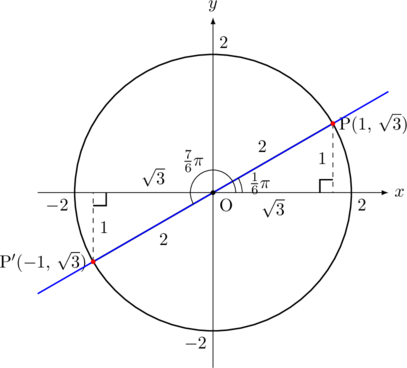
問題の答えは, 図からわかるように,
 数樂管理人のブログ
数樂管理人のブログ 

