こんにちは。今回は少なくとも1つの実数解を持つとはどんなことか見ておきます。
グラフがx軸と交わること
関数![]() が最高次数が奇数の関数で係数が実数ならば, 少なくとも一つは実数解をもつ。このことは, 微積分でこの性質を使って解法するときがあります。実際どうなんでしょう。
が最高次数が奇数の関数で係数が実数ならば, 少なくとも一つは実数解をもつ。このことは, 微積分でこの性質を使って解法するときがあります。実際どうなんでしょう。
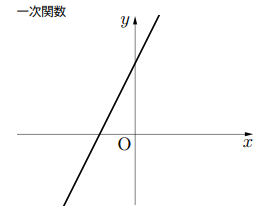
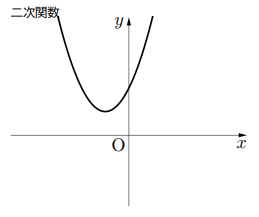
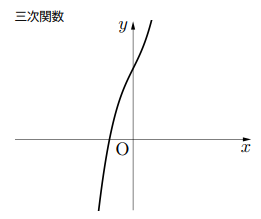
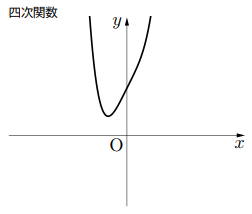
このように, 最高次数が偶数では![]() 軸との交点が存在しない場合が出てきます。ここで, 確認ですが, 関数
軸との交点が存在しない場合が出てきます。ここで, 確認ですが, 関数![]() が
が![]() 軸との交点をもつということは,
軸との交点をもつということは, ![]() となる
となる![]() が存在するということです。ここでは, 最高次数が奇数なら
が存在するということです。ここでは, 最高次数が奇数なら![]() となる
となる![]() が最低一つは存在するという確認です。
が最低一つは存在するという確認です。
ここで, ![]() は自然数)
は自然数)
とおくとき,![]()
である。またグラフは連続関数であるから, 中間値の定理より![]() となる
となる![]() が少なくとも一つは存在することが分かる。
が少なくとも一つは存在することが分かる。
ちなみに, 最高次数が偶数なら, ![]() は自然数)
は自然数)
とおくとき,![]()
となり, ![]() となる
となる![]() を確認できない。
を確認できない。
以上より最高次数が奇数の関数で, 係数が実数ならば, 少なくとも一つの実数解をもつ。
 数樂管理人のブログ
数樂管理人のブログ 

